THE FLOW AROUND A CIRCULAR CYLINDER
The theoretical investigation of the vortex pattern which is observed in the wake of a cylinder was originated by von Karman2-24 who considers a double row of vortices in a two-dimensional flow (Fig. 2.3). The equilibrium configurations (the patterns that can maintain themselves in the
flow) and the stability of the equilibrium configurations against infinitesimal disturbances, (displacements of individual vortices), are studied. It is found that the double row of vortices is stable only if the vortices in one row are opposite to points half way between the vortices in the other row, and if the distance between the rows is 0.281 times the distance between two consecutive vortices in each row. Such an arrangement of vortices is known as a Karman vortex street.
The theoretical treatment of the vortex street based on the assumptions of a perfect fluid cannot reveal the Reynolds-number effect, whereas measurements do indicate definite effect of the Reynolds number on the flow pattern.
In a flow past a long circular cylinder, a great variety of changes occur with an increasing Reynolds number* R. At low values of R the flow is smooth and unseparated, but the fluid at the back of the cylinder is appreciably retarded. At higher values of R two symmetrical standing vortices are formed at the back. With increasing Reynolds number these vortices stretch farther and farther downstream from the cylinder. Eventually the standing vortices become considerably elongated and distorted. When R reaches a number of order 40, the vortices become asymmetrical, detach from the obstacle, and move downstream as if they were discharged alternately from the two sides of the cylinder. In this way an eddying motion in the wake is set up. As the flow moves downstream, the eddying motion is gradually diffused and “decays” into a general turbulence. For R in the range of 40 to 150, the “shedding” of vortices is regular. The eddying motion in the wake is periodic both in space and time. The flow can be approximated by a Karman vortex street. The range of R between 150 and 300 is a transition range, in which the vortex shedding is no longer so regular as before. Its frequency appears to be somewhat erratic. For R > 300, the vortex shedding is “irregular.” A predominant frequency can be easily determined, but the amplitude appears to be more or less random. In addition, “background” random fluctuations, similar to turbulences behind a grid in a wind tunnel, becomes more appreciable. The kinetic energy of fluctuations in the wake is partly contained in the periodic motion and partly carried by the turbulences. As R increases, more and more of the energy is transferred to the turbulences. Finally, at R of order 3 x 10s, the separation point of the boundary layer moves rearward on the cylinder. The drag coefficient of the cylinder decreases appreciably owing to this important change (see Fig. 2.4). The flow in the wake at these large Reynolds numbers becomes so turbulent that the vortex street pattern is no longer recognizable.
The diameter of the cylinder is taken as the characteristic length.
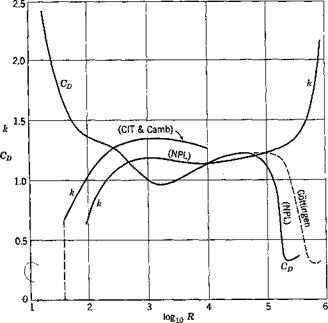
The geometry of the wake, when the Reynolds number is in a range in which vortices may be regarded as “shedding,” is as follows: The frequency at which the vortices are shed, expressed nondimensionally as the Strouhal number2 23 k, is a function of the Reynolds number. Here the Strouhal number к shall be defined[7] as cod/U, where to is the frequency in radians per second and d is the diameter of the cylinder. The results of Relf and Simmons2,25, Kovasznay2,26, and Roshko2’2′ are given in Fig. 2.4, from which the value of к for each R can be found. f The number
|
Fig. 2.4. Variation of the Strouhal number and drag coefficient against Reynolds number for a circular cylinder. CD and R are based on the diameter of the cylinder. Sources of data are: NPL; Relf and Simmons, Aeronaut. Research Com. R. & M. 917 (1924). Cambridge; Kovasznay, Proc. Roy. Soc. A. 198 (1949). CIT; Roshko, NACA Tech. Note 2913 (1953). Gottingen; Ergebnisse A VA Gottingen, 2 (1923). |
of vortices n = w/Itt, shed from each side of the cylinder, is
n = per second (1)
2irdv
The distance A between two consecutive vortices in a row is
U — v Iv
A=———- 0.25 to 01 (2)
n U /
where v is the relative velocity of the vortices with respect to the free stream. The ratio of the distance #hetween the rows of vortices to the distance A is approximated by von Karman’s theoretical formula H = 0.281A at small distance from the cylinder, but H/A increases as the distance from the cylinder increases. At large distance H/A is of order 0.9. The intensity of the velocity fluctuations is small close behind the cylinder. The maximum intensity of the fluctuations occurs in the vicinity of 7 diameters downstream. Thus it appears that the vortices are not really “shed” from the cylinder, but are developed gradually.
The range of Reynolds numbers of interest in aeroelasticity is the range in which the flow fluctuates, i. e., for R > 40. At a large Reynolds number, say R> 3 x 10®, or at a distance far downstream of the cylinder, although no distinct vortex pattern can be observed, the flow is turbulent and can still excite oscillations in an elastic structure.
In the subcritical Reynolds number range (R <3 x 10°), a periodic lift force (perpendicular to the flow) acts on the cylinder; the root-mean – square value of the lift coefficient (lift force/unit span)/(|pt/2-diameter), V=C?> is of the order of 0.45. In the Reynolds number range 0.3 x 106 to 3 x 106, the lift is no longer a periodic function of time, but becomes random, the root-mean-square value of the lift coefficient ranges from 0.03 if the cylinder surface is highly polished and the section is far away from a tip, to 0.13 if the surface is not polished. Near a tip of a structure aiarge variation of lift may occur. Thus a rocket with a spherical nose may have 4 or 5 times as much lift as one with a conical nose. The unsteady component of the drag coefficient at such large Reynolds number has a root-mean-square value of the order of 0.03. At Reynolds number greater than 3 x 10е, periodicity reappears in the wake and the mean drag coefficient rises again to 0.7 or 0.8.