The International Standard Atmosphere

An important point to remember is that the rotor performance and the performance of the helicopter as a whole is a function of the air density in which it is actually flying. This makes it problematic to predict or compare aircraft performance metrics unless the data are corrected to some standard condition. For example, decreasing density (increasing altitude and/or temperature) will result in a greater power required for the same aircraft gross takeoff weight (GTOW). To remedy this problem, the International Standard Atmosphere (ISA) has been established, which gives the height in a standard atmosphere corresponding to the properties of the air in which the aircraft is flying. The standards1 are defined in Minzner et al. (1959), the ICAO (1964), and NASA (1966), where a standard day at sea level is an air temperature, 7b, of 15°C (59°F, 288.16°K, 518.4°R) with a barometric pressure, po, of

2116.4 lb/ft2 or 101,301 N/m2 or 29.92 in (980 mm) of mercury or 1013.2 millibars.

The pressure in the atmosphere is a function of altitude (elevation), h, and the air density is a function of both altitude and temperature. The pressure in the standard atmosphere is defined relative to the standard conditions as

where h is in feet, and the density is defined by

— = a = (1 – 6.876 x 10~6h)4 265.

1 The ICAN standard may be used in many European countries.

While it is the density altitude that affects the performance of the helicopter, the advantage of using pressure altitude is that it is a function of the ambient pressure alone, and the value of hp can be read directly off the altimeter in the aircraft. This is done by setting the value in the altimeter Kohlsman (reference) window to the standard sea level pressure

Altitude (ft)	Altitude (m)	Temperature (°F)	Temperature (°С)	Density ratio (p/Po)	Pressure ratio (P/Po)
0	0	59.0	15.2	1.0000	1.0000
1,000	304	55.4	13.2	0.9771	0.9644
2,000	609	51.9	11.2	0.9428	0.9298
3,000	914	48.3	9.3	0.9151	0.8962
4,000	1,219	44.7	7.3	0.8881	0.8637
5,000	1,524	41.2	5.3	0.8617	0.8320
6,000	1,828	37.6	3.3	0.8359	0.8014
7,000	2,133	34.0	1.3	0.8106	0.7716
8,000	2,428	30.4	-0.6	0.7860	0.7428
9,000	2,743	26.9	-2.6	0.7620	0.7128
10,000	3,048	23.3	-4.6	0.7385	0.6877
11,000	3,352	20.1	-6.6	0.7155	0.6614
12,000	3,657	16.52	-8.6	0.6932	0.6360

Table 5.1. Useful Values for the International Standard Atmosphere

Bhp^5-256 ) 0.001981 hp5256 288 Л6 /

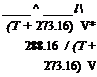of po = 29.92 inches or 1,013.2 millibars (equivalent to 2,116.4 lb/ft2 or 101,301 N/m2). Density altitude, however, must be computed from measurements of pressure altitude cor­rected for nonstandard ambient temperature. The density ratio can be obtained from

where the pressure altitude, hp, is in feet and T is in °С or using

p _ 518.4 / 0.001981 hp

~Po ~ (T + 459.4) V 288.16 )

where hp is in feet and T is in °F. Pressure altitude and density altitude are identical if the temperature conforms to standard conditions. As a rule of thumb, density altitude exceeds pressure altitude by about 60 ft per °F (30 ft per °С) that the temperature exceeds the standard value.

A convenient table of values for the standard atmosphere is given in Table 5.1. For example, on a standard day the density ratio will be 1.0 at sea level and 0.888 at 4,000 ft. On a very hot day with a pressure (indicated) altitude of 4,000 ft but with an outside air temperature of 30°C (86°F), which corresponds to approximately 23°C or 41°F over standard conditions, the density ratio will be 0.82. This corresponds to a density altitude of approximately 6,400 ft. Performance charts in a helicopter flight manual may be expressed in terms of either pressure altitude or density altitude, although pressure altitude is the more common form. Because the aircraft altimeter will read pressure altitude, a simple altitude conversion chart is provided to the pilot to allow rapid conversions to density altitude for a given ambient temperature, as required.

Aircraft gross takeoff weight – lb