THE REMAINDER OF h*

The remainder of h* ordinarily comes from the motion of hinged parts and from elastic deformation, although there are other kinds of possible relative motion, such as fuel sloshing which is important in liquid-fueled rockets (ref. 5.14). This total remainder is denoted by he. We now show that it is possible always to choose a set of body-axes FB for which he vanishes. These are termed “mean axes” by Milne (ref. 5.2).

Consider two centroidal reference frames FBi and FB^ for which the angular momenta are

hBl = RBlR£l dm + SBl(aBi+ 2 hr‘Bi (a)

*’ (5.4,25)

Ьд2 = J dm + + Ao>)Ba + 2 hr*B2 (6)

Here the summations are the contributions of spinning rotors, R in the inte­grals represents the residual relative motion, and Ato is the angular velocity of FB relative to FBl. The first term of (5.4,256) can be transformed as

140 Dynamics of atmospheric flight follows:

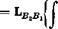H /gil dm “bj 11 /;, Ato^R^ dm Applying (5.4,17) to the last term, we get

he_B; = l^Bjj RbjRbj dm + в у AwjBjj (5.4,26)

It follows that the angular momentum b. eBi of the distortional relative motion vanishes in FB^ if

j dm + -&bx AtoBi = 0

or if

Awjjj = —SBfdm (5.4,27)

Equation (5.4,27) provides the condition that the axis system FB must satisfy if the angular momentum hBj referred to it is to have the form

К=-*1^в + 1Ъив (6.4,28)

І

This condition will be met when FB has the orientation required by TjBiBJt) that satisfies the differential equation [see (4.6,6)]

(5.4,29)

It is not necessary actually to solve (5.4,27 and 29) for LgiBa in order to make use of mean axes. Our concern here is simply to establish their ex­istence. We note that when the body axes are mean axes, the following relations must hold for the distortional motion. Since the origin is the mass center,

J* x’ dm —jy1 dm = J"s’ dm = 0 (a)

and from (5.4,23) (5.4,30)

J” (yz’ — y’z) dm = j (zx! — z’x) dm = J* (xy’ — xy) dm = 0 (6)

in which the prime denotes the distortional component of the velocity relative to FB. The use of mean axes, and the consequent elimination of distortional contributions to h* has the effect of eliminating the main inertial

coupling between the distortional degrees of freedom and those of the rigid body. Some coupling still remains through jP however, see (5.6,7).