Transport of Energy

Governing Equations. Energy is a scalar entity. Energy transport is de­scribed by means of the energy equation. From the many possible formula­tions, see, e. g., [2], we choose for our initial considerations the conservative flux-vector formulation (we assume here also two-dimensional flow)[36]

The term on the left-hand side represents the rate of increase of energy in the unit volume with time, the term on the right-hand side the gain of energy.

The internal energy of our our model air—a mixture of thermally perfect gases—is defined by

e (T, p) = cv (T, p) dT.

It is composed of the contributions of the molecular (im) and the atomic (ia) species

nm na

e ^ eim | ^ ^ &ia Є^а,

im = 1 ia = 1

which have the parts (see Section 5.2)

etranSim + erotim + evibr^m + eelim + AЄІ

and

eia = etransia + eelia + Aeia. (4.55)

etrans is the translation, erot the rotation, evibr the vibration, eel the electronic excitation, and A e the zero-point or formation energy [3].

V is the magnitude of the velocity vector

V = |V|. (4.56)

The symbol V in eq. (4.51) is the Nabla operator

q = р(є + l-V2)V +q + pV +т-V. (4.58)

—Є Z — —

The first term on the right-hand side of this relation represents the con­vective transport of energy into the unit volume, the second the molecular transport of energy, the third the work on the fluid by pressure forces (com­pression work), and the last by viscous forces (dissipation work).

The molecular transport of energy, q, in general, i. e., chemical non­equilibrium included, has two parts:

n

q = – kVT • (4.59)

І= 1

The first stands for the molecular transport of thermal energy (heat con­duction), and the second for the transport of thermal energy by mass diffusion due to chemical non-equilibrium of air as a mixture of thermally perfect gases. In eq. (4.59) hi is the enthalpy of the species i

hi = cPi dT, (4.60)

and j the diffusion mass flux.

—I

We find the heat transported towards the body surface, qgw, from the y-component of the energy-flux vector at the wall

If vw = 0, that is without suction or blowing at the wall, this equation reduces to

The first term is the classical heat-conduction term, the second the heat transport in chemical non-equilibrium flow, and the third finally a heat flux, which in the slip-flow regime appears in addition to the two other fluxes [21]. This third term of course disappears for non-slip flow.

Peclet Number, Prandtl Number, Lewis Number, Eckert Number, and Thermal Boundary-Layer Thickness. Noting that the energy flux is a scalar entity, we compare now—in the same way as we did it for the momentum flux—the convective and the molecular flux in x-direction.

To ease the discussion we introduce a simpler, and more familiar form of the energy equation in terms of the enthalpy h [2]

dq. v _ d%_ dp dp

dx dy dt dx dy

du dv du dv

rra—+TTO—+ гж,(—+ —)

By adding to the left-hand side of this equation the global continuity equation times the enthalpy we find, while expressing the mass-diffusion energy-transport term in eq. (4.59) for a binary gas, the conservative form of convective and molecular transport

Assuming perfect gas with h = cpT, and not anticipating a thermal bound­ary layer, we compare the convective and the conductive transport in x – direction (the first two terms in the first bracket on the left-hand side) after introduction of the simple proportionality дТ/дх ж T/L:

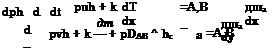pucpT pucpT pucpL ncp puL

—– — (Y ——– = —— = H P = ———- = НГ П P

k(dT /dx) k(T/L) к к p

and find in this way the Peclet number:

and the Prandtl number:

= P1 = pcp Re к ‘

The Prandtl number Pr can be written

Pr_ dh = Р/Р

k/pcp a

where

k

a=— (4.69)

pcp

is the thermal diffusivity [5], which is a property of the conducting material. The Prandtl number Pr hence is the ratio ‘kinematic viscosity v = p/p’ to ‘thermal diffusivity a’.

Of interest are the limiting cases of of the Peclet number Pe (compare with the limiting cases of the Reynolds number Re):

— Pe ^ 0: the molecular transport of heat is much larger than the convective transport.

— Pe ^ to : the convective transport of heat is much larger than the molecular transport.

— Pe = O(1): the molecular transport of heat has the same order of magni­tude as the convective transport.

which is interpreted as the ratio ‘heat transport by mass diffusion’ to ‘heat transport by conduction’ in a flow with chemical non-equilibrium. In the temperature and density/pressure range of interest in this book we have 0.5 < Le < 1.5 [8].

If we non-dimensionalize eq. (4.63) without the time derivative, and with proper reference data (p is non-dimensionalized with pu2), we find

All entities in this equation are dimensionless. The new parameter is the Eckert number

u2

E= —= (7-l)M2, (4.73)

CpT

with the Mach number defined by eq. (4.38). The Eckert number is interpreted as the ratio ‘kinetic energy’ to ‘thermal energy’ of the flow.

For E ^ 0, respectively M ^ 0, we find the incompressible case, in which of course a finite energy transport by both convection and conduction can happen, but where no compression work is done on the fluid, and also no dissi­pation work occurs. For E = 0 actually fluid mechanics and thermodynamics are decoupled.

We compare now for Pe = 0(1) the convective transport of heat in x- direction puCpT with the molecular transport of heat in у-direction qy, an­ticipating a thermal boundary layer with the thickness 5T. We do this in the differential form given with eq. (4.64)

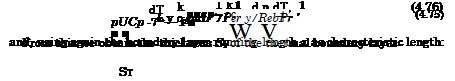
Again we introduce in a schematic way characteristic data and find after rearrangement

St k 1 1

— OC j ——— oc oc =

x Cppux Pex RexPr

The thickness of the thermal boundary layer St is related to the thickness of the flow boundary layer S = Sfiow by

— Pr ^ 0: the thermal boundary layer is much thicker than the flow boundary layer, which is typical for the flow of liquid metals.

— Pr ^ to: the flow boundary layer is much thicker than the thermal bound­ary layer, which is typical for liquids.

— Pr = O(1): the thermal boundary layer has a thickness of the order of that of the flow boundary layer. This is typical for gases, in our case air. However, since in the interesting temperature and density/pressure domain Pr < 1 [8], the thermal boundary layer is somewhat thicker than the flow boundary layer. This is also of importance for the wall-normal discretiza­tion of boundary-layer methods, see, e. g., [4].

Boundary Conditions. The energy equation, either in the form of eq. (4.51), or in the form of eq. (4.63), has terms of second order of the tem­perature T in both the x – and the y-direction. Hence we have to prescribe two boundary conditions. Like for momentum transport, one is defined at the body surface, the other for external flow problems (far-field or external boundary conditions) in principle at infinity away from the body. In addition we have to prescribe boundary conditions for the heat transport by mass diffusion in chemical non-equilibrium flow, and by velocity slip, eq. (4.62).

First we treat the ordinary heat-flux term. We have seen in Section 3.1 that five different situations regarding the thermal state at the body surface

are of practical interest. Before we look at the corresponding boundary con­ditions, we consider the general wall-boundary condition for T in both the continuum and the slip-flow regime, Section 2.3.

The general boundary condition for T at a body surface reads [20][37]

Here a is the thermal accommodation coefficient, which depends on the pairing gas/surface material : 0 ^ a ^ 1. Specular reflection, which means vanishing energy exchange, is given with a = 0, and diffusive reflection, indi­cating reflection accommodated to the surface temperature Tw with a = 1. Specular reflection hence indicates perfect decoupling of the temperature of the gas at the wall Tgw from the wall temperature Tw, i. e., a ^ 0: (dT/dy)w ^ 0. For air on any surface usually a = 1 is chosen.

Eq. (4.79) can be written in terms of the reference Knudsen number Knref

= Xref /Lref

— the classical wall boundary condition in the continuum-flow regime:

Knref < 0.01: Tgw = Tw, (4.81)

— and the temperature-jump condition in the slip-flow regime:

0.01 < Knref < 0.1 : Tgw = Tw. (4.82)

Again the reference Knudsen number must be chosen according to the flow under consideration, e. g., for boundary-layer flow it would be based on the boundary-layer thickness. And also here it should be remembered that there are no sharp boundaries between the two flow regimes.

With regard to the boundary conditions, which represent the five different situations of the thermal state of the surface (Section 3.1), we consider only the continuum-flow regime case with Tw = Tgw and find:[38]

1. Radiation-adiabatic wall: qgw = qraci —>• кЩ-ш = eaT4.

2. Wall temperature at the wall without radiation cooling: Tw.

3. Adiabatic wall: qgw = 0 —>• = 0.

4. Wall temperature at the wall with radiation cooling: Tw, and qrad =

eaTw.

5. Wall heat flux (into/out of the wall material) is prescribed: qw = qgw –

qrad.

There remains to consider the energy transport by mass diffusion in chem­ical non-equilibrium flow. The wall-boundary conditions of the diffusion flux jiy will be treated in the following Sub-Section 4.3.3. Important are the cases of finite and full catalytic recombination of atoms at the surface, Section 5.6. Catalytic recombination enhances strongly the heat transport towards the surface. On the one hand this is due to the release of dissociation energy in the recombination process. On the other hand, since the atomic species disappear partly or fully at the surface, the mass-diffusion flux as such is enlarged.

Finally the velocity-slip term in eq. (4.62) is recalled. The corresponding boundary conditions are found in Sub-Section 4.3.1.

Regarding external boundary conditions the same holds for the energy equation as for the Navier-Stokes equations. Special situations exist for in­ternal flows, e. g., in inlets, diffuser ducts etc., which we do not discuss here.