Transport of Mass

Governing Equations. Mass is a scalar entity. Mass transport is described by means of the (global) continuity equation (two-dimensional)

, (V) , = 0

dt dx dy

The first term on the left-hand side represents the rate of increase of mass in the unit volume with time, the second and the third term the gain of mass by convective transport.

In the case of chemical non-equilibrium we have a “species” continuity equation for every involved species [2]15

dfH dp. jU dpi’v dt dx dy	‘4/ ‘4/ . dx dy
+ Smi	(4.84)

The terms in the bracket on the right-hand side represent the mass trans­port by diffusion, and Smi the source term of the species, Section 5 and Appendix A. The terms jix and jiy are the components of the mass-flux vector j. of the species i. This diffusive mass-flux is a flux relative to the con­vective (bulk-flow) mass flux pV_ [2]. Summation over all species continuity equations (4.84) results in the global continuity equation (4.83).

Hence we have the global and n species continuity equations, one more than needed. In praxis one can use the superfluous equation for an accuracy check.

The diffusion mass-flux vector, which we have mentioned already in the preceding Section 4.3.2, has four parts [2]

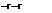(4.85)

For convenience we write these four parts in terms of a binary mixture with the species A and B:

— Mass diffusion due to a concentration gradient VcoA (Fick’s first law)

1{A = ~1{B = – pDabY^a-

— Mass diffusion due to a pressure gradient Ypa

— Mass diffusion due to a temperature gradient VTA (DJ is the thermo­diffusion coefficient)

lT = ~Ib] = -^Da^- (4-88)

— Mass diffusion due to body forces

£а=-£в – (4-89)

Of these four diffusion mechanisms the last two usually can be neglected in aerothermodynamics. Pressure-gradient diffusion may play a role in oblique shocks [21], curved nozzles, etc. In aerothermodynamic diffusion problems we deal with multi-component mixtures, hence we have to use generalized relations, given for instance in [2].

Finally we write eq. (4.84) in conservative form, and in terms of the mass fraction шр.

Schmidt Number and Mass-Concentration Boundary-Layer Thick­ness. Noting that mass is a scalar entity we compare now, in the same way as we did for the energy flux, the convective and the molecular flux in x – direction, however only in terms of binary concentration-driven diffusion, eq. (4.86)

and find the Schmidt number

pDab

This number is related to the Lewis number Le via the Prandtl number Pr

L _ Dr _ рсрРлв _ Dab Sc к a

The following limiting cases of Sc can be distinguished:

— Sc ^ 0: the molecular transport of mass is much larger than the convective transport.

— Sc ^ to: the convective transport of mass is much larger than the molecular transport.

— Sc = O(1): the molecular transport of mass has the same order of magni­tude as the convective transport.

We compare now for Sc = O(1) the convective transport of mass in x- direction (мхи with the molecular transport of mass in у-direction jy, antic­ipating a mass-concentration boundary layer with the thickness 5M. We do this in the form given with eq. (4.84) after introducing the mass fractions xa and xb

	д дшА + – a~(pDab—s— ду ду
(4.94)

Again we introduce in a schematic way characteristic data and find

5м I Dab 1

L °V uL * y/ReLSc

and in terms of the boundary-layer running length x [39]

We can distinguish again three cases:

— Sc ^ 0: the mass-concentration boundary layer is much thicker than the flow boundary layer.

— Sc ^ to: the flow boundary layer is much thicker than the mass-concentra­tion boundary layer.

— Sc = O(1): the mass-concentration boundary layer has a thickness of the order of that of the flow boundary layer.

The above discussion has shown that mass transport can be described analogously to momentum and energy transport. However, the discussion is somewhat academic regarding thermo-chemical non-equilibrium flows, be­cause mass transport is not necessarily dominated by the surface boundary conditions (the thermal state of the surface), like in the case of the other entities. An exception possibly is the flow of a strongly dissociated gas past a fully catalytic surface.

Boundary Conditions. The global continuity equation, eq. (4.83), has first – order derivatives of the velocity components u, v, and the density p only. At the body surface the boundary conditions for u and v are those discussed for momentum transport in Sub-Section 4.3.1. For the density p, like for the pressure p, only a wall-compatibility equation, i. e., no boundary condition, can be prescribed at the body surface [4, 17]. Hence, if an explicit boundary condition is necessary for p, it must be described at the far-field or external boundary.

The situation is different with the species-continuity equations (4.84), (4.90). Here we have second-order derivatives with each of the diffusion­driving mechanisms. Regarding the boundary conditions at the body sur­face we note without detailed discussion four possible general cases (see also Section 5.6):

— equilibrium conditions for the species

= Ui(p, T )|ш ,

— vanishing mass-diffusion fluxes

jiy W 0,

— fully catalytic surface recombination

Шatomi lw °

— finite catalytic surface recombination (kw is the catalytic recombination rate at the wall)

Шi (kw i p, T) •

Regarding far-field or external boundary conditions the same holds for the continuity equations (global and species) as for the Navier-Stokes equations and the energy equation.