Typical Trim Solution Procedure for Level Flight

In the trim process, the rotor collective and cyclic pitch controls must be adjusted to control the orientation of the rotor to provide trim, control and propulsion requirements. For wind-tunnel trim, the rotor cyclic controls are calculated from a prescribed rotor shaft angle (say, equivalent to Op). In a wind tunnel, the model rotor is controlled by a conventional swashplate and the operator remotely “flies” the model rotor very much in the way of an actual helicopter. However, because the rotor is rigidly attached to a support system, the operator must ensure that large amounts of cyclic flapping do not occur as the wind speed is increased. This is done by constantly controlling the orientation of the swashplate to eliminate cyclic flapping with respect to the rotor shaft. A typical free-flight trim simulation is more complicated because it must satisfy the vehicle equilibrium equations and involves the following steps:

which is valid for p, > 0.1. For lower advance ratios, we should use the more complete expression

СРш = 2y/iJM+X2 + ^ + 4,65+ 2 (a) ^ + XcCtmr’ (4-123)

where the iterative numerical procedures to solve the general inflow equation that have been discussed in Section 2.14.3 can be used to determine X.

3. Calculate the tail rotor thrust from the torque balance using

ytr _ cQMr r _ cpMr r w cTmr 1t Ctmr h

4.

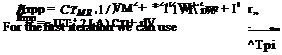Calculate the inflow, Xjpp using

5. Calculate the drag and side forces using Eqs. 4.113 and 4.114. For the first iteration, set C^p = Cy^p = 0.

6. Calculate fc, (3s, 0F, and фр.

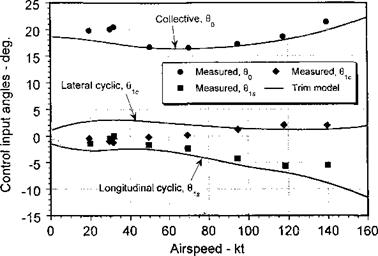
Figure 4.25 Representative variations in collective and cyclic pitch inputs to trim a rotor in forward flight. Propulsive trim calculation. Data source: Ballin (1987). (Calculation courtesy of Rendy Cheng.)

7. Calculate во, 0s, fio, and 6c.

8. Go back to step 3 and recalculate the values.

9. Iterate and monitor the control angles until convergence is achieved.

Representative variations in the control input angles, 6q, 9c, and 9s versus forward speed for a conventional helicopter, as computed from a typical free-flight trim solution, are shown in Fig. 4.25. The results must be considered representative only but are typical of the inputs that would be required on any single rotor helicopter. An example helicopter, which resembles the UH-60, was used for these calculations. Experimental measurements of control angles are also shown, which are taken from Ballin (1987). Remember that as the rotor transitions from hover to forward flight, a primary effect is the dissymmetry in lift between the advancing and retreating blades. The excess of lift on the advancing blade causes the blade to flap upward, reaching a maximum displacement over the front of the disk. Conversely, the reduced dynamic pressure on the retreating blade causes the blade to flap downward over the rear of the disk. The net effect is that the rotor disk naturally wants to tilt back (i. e., a negative longitudinal flapping or Therefore, to prevent this longitudinal

flapping, the cyclic pitch controls must be adjusted to bring the rotor disk back to an orientation that will meet propulsion (to overcome vehicle drag) and control requirements. Notice that the 9s component of cyclic pitch (longitudinal cyclic) controls the longitudinal flapping; thus an increasingly negative value of 9s (of magnitude approximately equal to — file) must be imposed by using forward stick.

The effects of blade coning cause a lateral flapping response. When a blade passes over the front of the disk, the effects of the forward flight velocity cause an increase in AoA because it acts as an upwash. At the rear of the disk, the effects of the free stream cause a decrease in AoA. Therefore, there is a once-per-revolution (1/rev) forcing function gener­ated as a result of blade coning, and the response to this forcing causes a negative lateral disk tilt (to starboard). The amount of lateral tilt is proportional to the rotor coning angle, which in turn depends on inflow for a given rotor thrust. To counteract this effect, a positive value of lateral cyclic (9c) must be applied using left stick. A small additional amount

of lateral cyclic must also be applied to counter the thrust and moments produced by the tail rotor, which will vary with the anti-torque requirements. Also, some lateral cyclic is required to compensate for the nonuniformity of the longitudinal inflow over the rotor disk in forward flight (see Section 3.5.2). Because of these coupled effects, the amount of lateral cyclic required for trim does not show a strong trend in one direction unlike the longitu­dinal cyclic. See Harris (1972) for a systematic study of inflow effects on rotor flapping response.

V~/lld|Jl. Cl ivcvicw

A basic understanding of the dynamic behavior of the rotor blades in response to the changing aerodynamic loads has been the objective of this chapter. The blades have two primary degrees of freedom: flapping and lagging, which take place about either mechanical or virtual hinges near the blade root. A third degree of freedom allows pitch or feathering of the blade, which can be applied in both a collective and cyclic sense. Despite the fact that helicopter blades are relatively flexible, centrifugal effects cause stiffening and the basic physics of the blade dynamics can be explained by assuming them as rigid. In hovering flight the airloads do not vary with azimuth, therefore the blades flap up and lag back with respect to the hub and reach a steady equilibrium position under a simple balance of aerodynamic and centrifugal forces. However, in forward flight the fluctuating airloads cause continuous flapping motion and give rise to aerodynamic, inertial and Coriolis forces on the blades that result in a dynamic behavior with an amplitude and phase response. The flapping hinge allows the effects of the cyclically varying airloads to reach an equilibrium with airloads produced by the blade flapping motion. It has also been shown that the flapping motion is highly damped by the aerodynamic forces so the blades flap and the rotor tilts almost immediately in response to control inputs.

A rotor blade has a flapping natural frequency that is equal to its rotational frequency (or nearly so). Because the rotor is excited by the aerodynamic loads primarily at 1/rev, this means that there is a 90° phase lag between the aerodynamic forcing and the blade flapping response. It has been shown how collective and cyclic pitch can be used to change the magnitude and phasing of the aerodynamic loads over the disk. This is the key to changing the flapping of the rotor and the orientation of the rotor plane, thereby effecting a means of control for the helicopter. The ideas of controlling the orientation of the rotor are formally embodied in a procedure known as “trim.” While there are many forms of numerical solution to the trim problem, the basic procedure is the same: to adjust the control inputs to give resultant forces and moments on the helicopter that will satisfy a specified equilibrium and propulsive force condition. The evaluation of the various forces and moments acting on the helicopter is by no means trivial. However, under certain assumptions and with sufficient labor, many of the results can be obtained analytically in closed form. This allows the identification of the relationships between the solution and various problem parameters and will be useful for many problems related to the preliminary design of the helicopter.