2D Far-Field Approximations

The lumping process described in Section (2.3) made ad-hoc simplifications to the kernel functions, which introduced some unknown amount of error in the resulting simplified velocity fields. In this section the kernel function approximation will be made more precise by using a Taylor series. This will give the option of increasing the accuracy of the lumped model, and will also give insight into the behavior of the far-field, or flow-field far from the body. The detailed derivation will be performed for the velocity potential in the 2D case for simplicity. The corresponding 3D results will be summarily presented in the next section.

2.10.1 2D source and vortex distribution far-field

-JJ(* In R- ІП л/(x — x’)2 + (Z

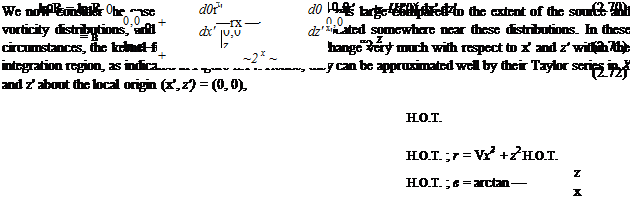By combining and recasting (2.50) and (2.53), arbitrary distributions of source and vorticity in 2D are seen to have the following perturbation potential field p, as sketched in Figure 2.14. The ln R and 0 kernel functions are defined for convenience.

where H. O.T. denotes higher-order terms with, z, z, x /3, etc. Substituting these Taylor series into the <p(x, z) integral (2.70) above, and rearranging gives

2ж tp(x, z) = ff jcr^lnr — Z-x’ — 4-2^ + u) (^—6 – + ~2 z’^j + H. O.T. j ёж’ dz’

with (2.73) being the result after the powers of x and z are collected and taken outside the x/z/ integrals. In terms of the convenient shorthand definitions

Л =	a dx/ dz/		(2.74)
Г =	fj w dx/ dz/		(2.75)
Kx =	jj {—ax’ + wz/)	dx/ dz/	(2.76)
Kz =	(—az/ — wx/)	dx/ dz/	(2.77)

equation (2.73) is a far-field expansion for the perturbation potential

Л Г кх x kz z

LO(x, z) ~ ,z) = — nr – ——- 6 +———- FT +—— FT

* 2тг 2тг 2тг г2 2тг г2

which is approximate because the higher-order terms have been dropped from the Taylor series. Taking the gradient and adding the freestream part gives the corresponding far-field expansion for the total velocity.

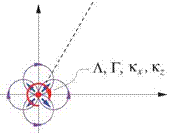
Replacing the exact velocity V(x, z) with the approximate Vff(x, z) is equivalent to replacing the a and w distributions with the corresponding Л, r, Kx, Kz, filaments as indicated by Figure 2.15. These Л and Г are

equivalent to those obtained by the lumping procedure described in the previous sections. However, the added doublet kx and kz terms are new, and can be considered as corrections for the errors due to lumping in cases where the the chosen lumped source and vortex location is offset from the centroids of the a and ш distributions.

z

Figure 2.15: Far-field approximation obtained by replacing a(x, z) and w(x, z) distributions or sheet Л(s) and j(s) configurations with the much simpler filament singularities.

For cases where the starting distributions arc source and vortex sheets with strengths A(s) and 7(s), the far-field coefficients would be defined as Л = f Л ds (2.80) г = f y ds (2.81) kx = 1 (-Лж’ + jz’) ds (2.82) Kz = 1 Ї. r. . / / (-Лг’ – jx’) ds (2.83) where the parametric functions x'(s), z'(s) specify the sheet geometry or geometries. The integrals are eval­uated over all the sheets present.

Application of the far-field potential or velocity expressions (2.78) or (2.79) requires knowing the values of the coefficients Л, Г, kx, kz. However, obtaining these from their definitions (2.80)-(2.83) is not possible in the typical situation where the field stregths a, ш or sheet strengths Л, 7 are not known without addi­tional information or modeling. The subsequent sections will describe alternative means for computing the coefficients from other relevant properties of the aerodynamic body.

2.11.2 Far-field effect of lift and drag

As derived in detail in Appendix C, the far-field vortex and source are related to the airfoil lift/span L’ and drag/span D’, or equivalently to the 2D lift and drag coefficients a and Cd based on the airfoil chord c.

	T!	1
г =			(2.84)
	pVco	2
	n1	1
Л =			(2.85)
	pv^	2d

Relation (2.84) is the well-known Kutta-Joukowsky lift theorem. Relation (2.85) is perhaps less familiar, but can be considered as the complementing theorem for the drag. Note that unstalled 2D airfoils typically
have Cd ^ C and thus Л ^ Г, and hence the vortex term dominates the source term in typical airfoil far-fields. In contrast, the source term is dominant for 2D bluff-body flows which typically have large drag and comparatively little or no lift.