A TWO-DIMENSIONAL EXAMPLE

Wing divergence is a simple example of the steady-state aeroelastic instability. If a wing in steady flight is accidentally deformed, an aero­dynamic moment will generally be induced which tends to twist the wing. This twisting is resisted by elastic moment. However, since the elastic stiffness is independent of the speed of flight, whereas the aerodynamic

moment is proportional to the square of the flight speed, there may exist a critical speed, at which the elastic stiffness is barely sufficient to hold the wing in a disturbed position. Above such a critical speed, an infini­tesimal accidental deformation of the wing will lead to a large angle of twist. This critical speed is called the divergence speed, and the wing is then said to be torsionally divergent.

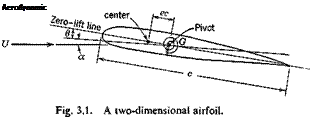
As a two-dimensional example, let us consider a strip of unit span of an infinitely long wing of uniform cross section. As shown in Fig. 3.1, let the elastic restraint imposed on this strip be regarded as a torsional spring with an axis at a point G which is fixed in space. The airfoil can rotate only about G. Assume that the spring is linear so that the torque is directly proportional to the angle of twist. Initially the “zero-lift” line of the airfoil coincides with the direction of the undisturbed flow. Let the entire system be first rotated through an angle a as a rigid body; then let the constraint be released to allow the wing to deflect elastically through an additional angle в. It is desired to find the equilibrium position of the wing (i. e. the angle в) in a flow of speed U.

The action of the aerodynamic force on the airfoil can be1 represented by a lift force, acting through the aerodynamic center, and a moment
about the same point. Let us write the distance from the aerodynamic center to the axis of the torsional spring as ec, c being the chord length and the factor e being a ratio expressing the eccentricity of the aerodynamic center (positive if the spring lies behind the aerodynamic center). Now the lift coefficient C; is proportional to the angle of attack, whereas the coefficient of moment about the aerodynamic center Cm0 is practically independent of the angle of attack.[9] Hence, the lift and moment per unit span acting on the airfoil are, respectively,

U = qCtc = qca{6 – f a) tt ~ ‘

M0′ = qCrnS)c2 (about aerodynamic center)

where a is the lift-curve (C, vs. a) slope, q is the dynamic pressure {pU2), a is the initial angle of attack, and в is the angle of twist.

The aerodynamic moment per unit span about the axis of the spring is therefore

Ma’ = M0′ + L’ec = qc2Cm0 + qec2a(0 + a)

= qec2ad + qec2a(ry. + Cm0/ea)

In the above equation a, is measured from the zero-lift line of the airfoil. If we define a direction corresponding to an angle — a0 = CmJea as the “zero-moment” line, and redefine the angle a as measured from the zero-moment line (i. e., take a as zero when the free stream direction coincides with the zero-moment line), then Eq. 2 becomes

Ma’ = qec2a(6 + a) (3)

When equilibrium prevails, the aerodynamic moment is balanced by the elastic restoring moment. Let IQ be the spring constant, so that the elastic restoring moment per unit span, corresponding to the twisting angle в, is Кав. On equating this with the aerodynamic moment given by Eq. 3, and solving for в, we obtain

qec2aat Kx — qec2a

For a given nonvanishing a, the angle в will increase when dynamic pressure q increases. When q is so large that the denominator tends to
zero, the angle d becomes indefinitely large, and the airfoil is “divergent.” Hence, the condition of divergence is

K« – qec2a = 0 (5)

The dynamic pressure at divergence qdiv and the divergence speed Udly are given by the equations

Ka. ,, ГЖ

Чйіч _ ec2a End Udiv V pec*a (6)

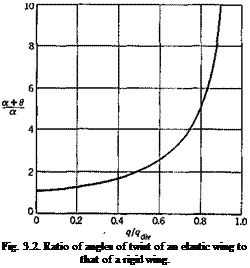
If the wing were infinitely rigid, Kx-> со; then 0 = 0. The ratio of the total equilibrium angle of attack a + в of an elastic wing to that of a rigid wing is, according to Eqs. 4 and 6,*

* [10] – ?/?div

This ratio is illustrated in Fig. 3.2. It is seen that the deflection of the elastic wing tends to be very large when q -»qdiy. When the speed of

flight is 80 per cent of the divergence speed, qlqdlv — 0.64, the wing twist is already 1.8 times the angle of attack of a rigid wing.

We may also take a different point of view as follows: Suppose that the airfoil of Fig. 3.1 be in equilibrium, so that d is given by Eq. 4. Let us ask whether this equilibrium configuration is stable. An equilibrium configuration is stable if there is a tendency to return to the equilibrium position, should the equilibrium be slightly disturbed. To test the sta­bility of the equilibrium configuration described by Eq. 4, let d be given an additional infinitesimal displacement Дd. Then the change in the aerodynamic moment is, from Eq. 2,

ДMa = qec2a Ad (8)

and that of the elastic restoring moment is

am; = Ка А в (9)

Now, if the change in the elastic restoring moment is larger than that of the aerodynamic moment, the wing will tend to return to its original position. So the equilibrium is stable if

am; > am;

If we follow the same argument, the wing will be unstable if the inequality sign reverses. The critical condition is then

am; = am; (io>

І. Є.,

qec2a AO — Ka Ad

which gives the same critical speed as Eq. 6.*

Note that AM; and AM; given by Eqs. 8 and 9 are independent of « and d. ‘Therefore the critical condition (Eq. 10) can be derived by assuming к and d to be zero. Hereafter we shall interpret d, Ma’, Me’ as the changes from the initial equilibrium values’, the symbol Д will be omitted.

Equation 6 shows that the critical divergence speed increases with increasing rigidity of the spring and decreasing chord length and eccentricity.