APPLICATIONS

The computation of the LFT models of the missile and transport air­craft is detailed in this chapter.

1. THE MISSILE

1.1 A PHYSICAL REPRESENTATION

In the same way as at the end of the previous chapter, the para­metric uncertainties in the stability derivatives are directly introduced in the physical missile model. Figure 4.1 represents equations (2.11) of the linearized missile model, with multiplicative uncertainties Si being introduced in the stability derivatives MQ, Ms, Za and Zs (i. e. MQ is e. g. replaced by (1 – t – 6)Ма). Note that the tail deflection input £ is renamed as и in this figure, in order to avoid any ambiguity with the vector <5 of parametric uncertainties.

The LFT model of the missile is obtained as:

(4.1)

where Д = diag(6, 62,63,64) and His) is the transfer in Figure 4.1 between inputs [u, mi, m2, m3, W4] and outputs [77, q, z, Z2, 23, 24]. This LFT model is minimal.

For the sake of simplicity, only uncertainties in the 4 stability deriv­atives were introduced above. Nevertheless, it would be possible to in­troduce uncertainties in the other physical parameters in Figure 4.1. It is worth emphasizing that the missile equations (2.11) are affine with respect to uncertainties in the 4 stability derivatives Ma, Ms, Za, Zs – However, they are no more affine when considering additional uncertain-

Ties in The physical parameTers QS, d, jj^ss, у or j^, since producTs

such as Mass*v now appear. Thus, Morton’s method can not be applied in This new context. On the contrary, it is straightforward to introduce additional uncertainties in QS, d, у or in the missile model of

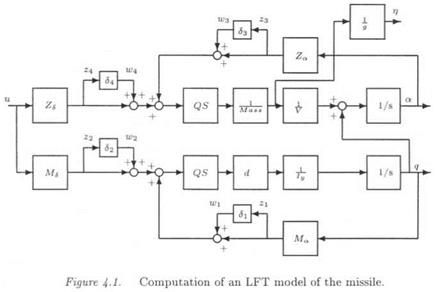Figure 4.1.