Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
CHAPTER V – CHARACTERISTICS OF. TRAILING-EDGE WING FLAPS
Flaps deflected downward from the tailing edges of wings, are primarily used to increase lift so that the landing speed can be reduced. They may also be used to improve performance during takeoff and when climbing. Available information on high-lift flaps is essentially statistical in nature. It is attempted in the following, to present the trailing edge flap characteristics as a function of pertinent parameters and to find methods of evaluation, beginning with two-dimensional sections and ending with configurations as they are used in operational airplanes.
I. LIFT CHARACTERISTICS IN TWO-DIMENSIONAL FLOW
Wing flaps as used in airplanes, are three-dimensional devices, limited in span, usually interrupted by the fuselage and interfered with by nacelles and propeller slipstreams (if any). The two-dimensional flow characteristics of flaps are the basis, however, from which more complicated configurations can be understood.
1. GENERAL
The problems connected with the design and analysis of trailing-edge flaps, in two-dimensional flow, are as follows:
• lack of, or complexity of theoretical methods,
• the amount of lift added by deflection of flaps,
• pitching moments affecting longitudinal trim,
• load distribution and hinge moments,
• stalling characteristics of flaps and airfoils,
• influence of Reynolds number on maximum lift,
• drag associated with the production of lift.
Analysis. The lift of thin airfoil sections correspond to CL = 2 tt sinor. Maximum lift is thus “expected” at ok = 90°, where practically all of that lift would be generated “at” the leading edge, by way of suction. The maximum lift coefficient would be in the order of CLX = 6. Deflection of a trailing-edge flap has two advantages: it reduces the need for higher angles of attack, and it gives the airfoil section “camber”, thus postponing flow separation from the upper side. Disregarding boundary-layer control (such as by suction) flow separation is evidently so strong at the larger angles of deflection needed that analytical efforts have been considered to be useless (l, e). However, with the use of high speed computation it is expected that methods will be developed to Find the performance of wings with flaps (2,g). Lift is generated in a wing, by deflecting a “tube” of the oncoming stream. To understand the mechanism of a trailing-edge flap, one may assume that the deflection corresponds to the direction into which the tail of the air foil section is pointing, or to which a not-too-small flap is deflected. Referring to Chapter IX, it may be said that (taking into account boundary layer effects) roughly:
dor /d6 =CJCLa = (cJcf ; 8<15° (1)
where n decreases from 0.7 at c^ /с = 0.1, to 0.6 at cf /с =
0. 3. This means that at a chord ratio c^/c = 0.2, for example, a deflection of the flap by 10f, produces almost the same lift increment as the airfoil or wing at an angle of attack of 5°. Equation 1 can only be used at small angles of flap deflection (say, up to 15°) as they may be used during takeoff and climbing of airplanes. Substantially to increase the maximum lift of a wing, much larger flap angles are required. Replacing the deflection angle 6 by its sine, and dot /d6 by sinS, we tentatively obtain
A Cl, =2тґsin(or +8(d(sincY )/d(sin&))) (2)
For (X = 0, it may then be true that
(aCl ) := 2 тґ sin (6" (sinb/SXdor /d6)) (3)
Tentatively again, it is assumed that d(sinot )/d(sinS) = dot /d6 as plotted in figure 2 of Chapter IX. For example, for do( /d6 = 0.5, as for cf/с = 0.20 or 0.25, we thus obtain a maximum
(лСи )x* 0.9 (2 tr) Sin(0.5 0.64 90)* = 2.7
These equations produce a flat maximum at 5 = 90° which seems to be compatible with experimental results on flaps with boundary-layer control by suction. However, flow separation (on plain and split flaps), boundary – layer and circulation losses (on slotted flaps) and increased or “super-circulation” (in particular when blowing over flaps) are bound to bring about negative or postive deviations from any simple theoretical formulation.
Types of Flaps. As illustrated in figure 1, a number of trailing-edge flaps have been developed, tested and used:
a) The ordinary or plain type (similar to control flaps) is rarely used as a landing flap. As mentioned above, the flow separates easily from the suction side. Maximum lift is not spectacular, drag is high because of separation and the wake is not necessarily stable.
b) Through the use of boundary layer control (suction) the separation from the plain flap can be eliminated. Characteristics would then be similar to those under (e).
c) The split flap was for many years used in the design of airplanes, particularly of fighters. This type is considered structurally simple. In terms of performance the lift is comparatively high and the drag connected with the “dead” space behind the flap, is evidently tolerable or even desirable during the landing operation.
d) The Zap flap (named after its inventor E. F. Zap) is a kinematic variation of the split type. Forces (moments) required for deflection are reduced, and maximum lift is increased (on account of an effective increase of wing chord).
e) The simple slotted flap (first or predominantly promoted by Handley Page) postpones separation to some 45° of deflection. Lift is increased, and drag is reduced.
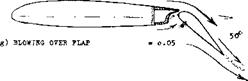
f) The “external” flap (developed and used at one time by Junkers) can be considered to be a slotted flap, with a very long and flat entrance.
g) The supply of “fresh” air through a slot can be replaced and considerably increased by blowing over the deflected flap.
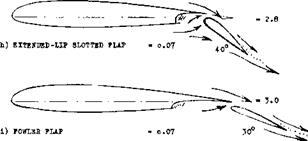
h) Shape of and flow through a slot are improved when extending the upper lip and translating the flap accordingly.
i) The Fowler flap (named after H. D. Fowler), combines the slotted feature as in (e) with an increase of the effective geometric airfoil chord; similar to (h).
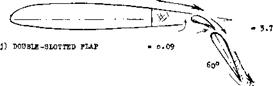
j) The ultimate in variable geometry are double-, triple-, or multiple-slotted devices, combining and fully utilizing the characteristics as under (e) and (i).
All of these types of trailing-edge flaps (and some similar devices) are discussed in this chapter.
Experimental Results. Wind-tunnel tests are usually carried out between Rc = 4(10) and possibly 6(10) . For a landing speed, say of 120 knots, and an assumed wing chord of 10 ft, the Reynolds number is in the order of Rc = 10 . Realistic simulation of full-scale conditions in wind tunnels thus seems to be possible. However, because of the particularly high lift coefficients tested, tunnel corrections are comparatively large; and it seems that these corrections (developed for lift coefficients, say up to unity) are no longer sufficient. It is shown in Chapter II that pitching moments due to camber as tested in the NACA two-dimensional setup (between walls in a closed test section) are evidently out of line. Although the procedure for correction lift-curve slope (2,b) includes a term corresponding to C™, it is suspected that this term is no longer adequate considering the extreme amounts of “camber” introduced by trailing-edge flap deflection. Another reason for the high lift increments observed in closed-type tunnels seems to be blockage by larger flap deflections and by the comparatively very large wakes (2,d) trailing from certain types of flaps. Corrected experimental results obtained in open-jet wind tunnels, exhibit, on the other hand, comparatively smaller lift increments due to flaps. This is possibly because of the curved deflection of the tunnel stream. We have corrected (2,c) some of the data evaluated and presented in this chapter to levels believed to be realistic.
Forces and Moments. When using trailing-edge flaps (at modest angles of deflection) during takeoff and when climbing, their performance efficiency (in terms of D/L or L/D) is most important. We will see what can be accomplished when using trailing-edge flaps for this purpose. — Loads due to flaps and on flaps are a justified concern of structural engineering. Pressure or load distributions, and the magnitude of the hinge moments due to deflection, will be presented. — Pitching moments due to flaps are a necessary evil connected with any successful type of trailing-edge flaps. It will be seen what their magnitude is, and how it can be reduced by three-dimensional “tailoring” of a wing.
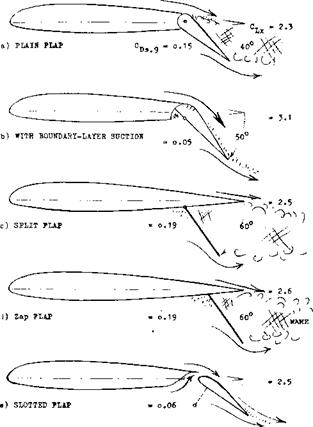Figure 1. Principal types of trailing-edge flaps, at an angle of deflection considered suitable in the landing operation of airplanes. The force and moment coefficients are estimated average values in two-dimensional flow, for 25% flap-chord ratio.
(1) Theoretical analysis of wing flaps:
a) Theoretical analysis applies primarily to small angles of deflection, and is as such treated in the “control-devices” chapter.
b) For some extension of analysis to higher angles of deflection, see (13,b).
c) Walz, Pressure Distribution Including Wake, Ybk D Lufo 1940 p 1-265.
d) Walz, Analysis of CLma)( German ZWB FB 1769 (1943); Cornell Trans 1951.
e) Some results of (c) and (d) are shown by Reigels in “Aerodymanische Profile”, Oldenbourg Munich 1958. Assuming wake or dead space behind a sufficiently deflected flap to have a certain size and shape, it is possible (c) to “predict” pressure distribution, forces and moments using potential theory. Of course, these characteristics have to be known first from experiments, before the agreement as shown can be obtained.
f) Davenport, Limits of Circulation in Three-Dimensional Flow, J A’Space Sci 1960 p 959. Earlier work on the subject by Helmbold & McCormick is referenced.
g) Stevens Mathematical Model for 2D Multi-Component Airfoils NASA CR-1843.
(2) 
Correction of wind-tunnel results:
a) It is not the purpose of this text to investigate wind-tunnel techniques. There is some difference, however, in the lift – curve slopes as reported for the two-dimensional setup (between walls) as in (13,a) and as derived from wings tested at A = 5 or 6 in open-jet tunnels such as in (13,b).
b) Procedures for correcting closed-tunnel results are reported in (13,a); see also Allen, Wall Inteference NACA TRpt 782 (1944).
c) As shown in Chapter II, the lift-curve slope depends upon parameters such as thickness ratio and skin friction (Reynolds number). Restricting ourselves to moderately thick and “conventional” airfoil sections, statistical experience seems to indicate that increments (ACU ) as tested in the NACA two-dimensional tunnels are too high (possibly by 4%), while those evaluated from the DVL open-jet tunnel are too low (possibly by 4%). Results in the various graphs of this chapter have been corrected accordingly.
d) Consider that the section-drag coefficient of an airfoil with 60 split flap is in the order of С^^ = 0.15, in comparison to less than 0.01 for the plain foil. As a consequence, blocking should have an effect upon lift due to flaps.
e) An example for blocking is NACA TN 3797 where an airfoil with 4.5 ft chord is tested between the walls of a closed tunnel which is 10 ft high, with a 30% plain flap deflected up to 70 . The increment for that angle is stated to be (дС|_) = 1.8, which is some 25% more than we would expect according to Figure 3.
