Circulation

Circulation is defined as the negative of the line integral (defined in mathematics in the counterclockwise sense) of the tangential component of the velocity vector around an arbitrary but fixed closed path in the velocity field, as illustrated in Fig. 4.4. By definition, then:

circulation = Г = – ф V • ds. (4.8)

Thus, a negative sign is introduced into the definition of circulation in Eq. 4.8 because, although mathematicians associate a positive result with a counterclock­wise integration, it is more convenient in aerodynamics applications to define posi­tive circulation as clockwise, as becomes apparent when applications are discussed later. Some authors omit the minus sign in Eq. 4.8 and assume the line integration to be in the clockwise sense. Thus, it is important to specify the direction of integration before evaluating the circulation for a given problem.

The evaluation of the line integral starts at an arbitrary point on the closed path and “marches” around that path in a counterclockwise direction. With each

Figure 4.4. Contour C and directed-line segment ds.

incremental step of length ds along the path, the velocity component in the direction of the line segment ds is multiplied by the magnitude of ds and the product noted. The line integral is the sum of all of these products. The integrand in the line integral, Eq. 4.8, may be expanded as:

V. ds = iViidsi cos (angle between).

As reviewed in Chapter 3, the vector-dot product is a component-taking operation. Thus, in the integrand of Eq. 4.8, the component of V in the direction of ds is multi­plied by the magnitude of ds as required by the line-integral definition. Note that ds here is an incremental line segment and not a unit vector. That is, ds = dx i + dy j + dz k.

In Cartesian coordinates:

Г = – Pc (мі + vj + wk) • (dx i+dyj + dz k)

C x (4.9)

or Г = – (pc [udx + vdy + wdz.

The circulation may be linked to the curl of the velocity vector and then to the vorticity in a flow by appealing to Stokes’ Theorem, which relates line integrals and surface integrals. By Stokes’ Theorem, if A is any vector, then:

pcA. ds = jj(Vx A). ndS,

s

where n is a unit vector everywhere perpendicular to S and the surface S is the area bounded by the curve C. Think of a closed wire frame, C, oriented in three-space. The surface S would be a diaphragm with edges along C; it need not be in the plane of C and may be of any arbitrary shape.

Letting A be the velocity vector V, Stokes’ Theorem states that:

Equation 4.10 links vorticity (i. e., particle rotation) to the magnitude of circu­lation. Later, a close link between circulation and airfoil lift is demonstrated. The concepts of vorticity, circulation, and curl apply to two – or three-dimensional, com­pressible or incompressible, viscous or inviscid flows.

EXAMPLE 4.4 Given: Consider a two-dimensional flow field given by V = (2y) i + (4x) j.

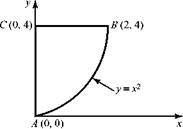Required: Find the circulation around the closed path A-B-C shown here by evaluating the line integral and by using Stokes’ Theorem.

Approach: Because two different methods are required, both the line-integral definition and Stokes’ Theorem are used.

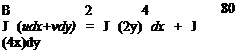Solution: Evaluating the line integral around the given closed path starting at point A:

because along A-B, y = x2 and so (2y)dx = (2×2)dx and (4xdy) = (4y1/2)dy:

C 0 4

B-C: J(udx+vdy) = J(2y)dx + J(4x)(0)dy = – l6, because along B-C, y = 4

B 2 4

A 0 0

and C = A: J (udx+vdy) = J(2y)(0) + J(4x)dy = 0, because along C-A, x = 0.

C 0 4

Now, utilizing Stokes’ Theorem:

Appraisal: The two results agree, as they should. Note that this flow is rotational. Also note that here, the curl of the velocity vector for this velocity field is a con­stant independent of x and y, so that the evaluation of the double integral simply amounted to calculating the area of the figure A-B-C. It is important to note that this is a special result; the value of the curl need not always be a constant independent of x and y.