Effect of Density Altitude

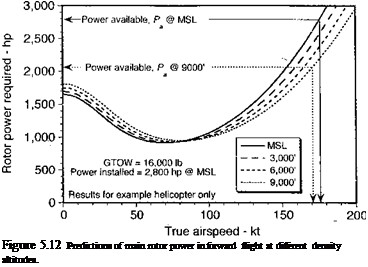
As discussed at the beginning of this chapter, an important operational consideration is the effect of altitude on overall helicopter performance. As shown in Fig. 5.12, increasing density altitude increases the power required in hover and at lower airspeeds. At higher airspeeds, the result of lower air density results in a smaller power requirement because of the reduction in parasitic drag. However, a higher density altitude will also affect the

«„пііпкіл a n їй сю :л Л1____________ псп?

engine avauaui^. rva suuwu in at 7,uva/ it inc puwci avauauic is auuui z, jtо

less than that available at MSL conditions, resulting in a large decrease in the excess power available at any airspeed relative to that at MSL.

5.5.2 Lift-to-Drag Ratios

The lift-to-drag ratio (L/D) of the helicopter or just the rotor alone can also be calculated from the power required curves. This is useful for comparison of the forward flight efficiency with another rotor, another helicopter, or a fixed-wing aircraft. Because the rotor provides both propulsive and lifting forces, the lift force is T cos orTPP. The effective drag can be calculated from the power expended (i. e., D = P/Vqq). For the rotor alone the power is P = Pi + Pq, and for the complete helicopter P = Р,- + Pq + Pp + Ptr – Therefore, for the rotor alone the lift-to-drag ratio is

L _ T cos (Xppp ^ WVoo D ~ (Pi + PqVVoo ** Рі + Pq’

For the complete helicopter the lift-to-drag ratio is

— = T cosa^ ~ WV°° (5 56>

D (Pi + Po + Pp + Pm)/Voo ~ Pi + Po + P/

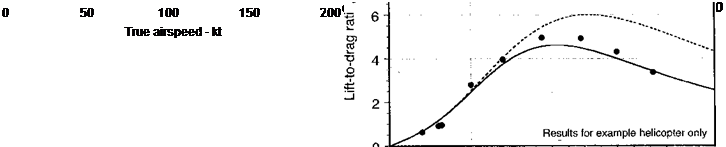
Representative results for the lift-to-drag ratio for the example helicopter in forward flight are shown in Fig. 5.13. It is apparent that the L/D increases rapidly as induced power requirements decrease, reaches a maximum, then drops off as the parasitic power

requirements rapidly increase. The maximum lift-to-drag ratio of the rotor is about 6, which is typical of most modem helicopters and is also typical of a low aspect ratio fixed wing. The maximum lift-to-drag ratio of the complete helicopter is about 4.5, which gives some idea as to the considerable effect of the airframe drag in the overall cmise efficiency of the helicopter. A typical L/D ratio for a fixed-wing aircraft of the same gross weight will be about 3-4 times this value. Note that the maximum lift-to-drag ratio for this example occurs at about 100 kts, which will be the airspeed to fly for maximum range. The lift-to-drag ratio of the rotor and helicopter will also be a function of the density altitude at which it is flying.

5.5.3 Climb Performance

The general power equation can be used to estimate the climb velocity, Vc, that is possible at any given airspeed. Rearranging Eq. 5.53 in dimensional form in terms of Vc leads to

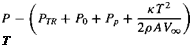
(5.57)

It is realistic to assume that for low rates of climb or descent the rotor induced power, Pi, the profile power, P0, and the airframe drag, D, remain nominally constant. In this case we can easily solve for the climb velocity to get

Note that Pievei is simply the net power required to maintain level flight conditions at the same forward speed. If the installed power available is Pa (which may vary with flight condition) then it will be seen that the power available to climb varies with forward flight

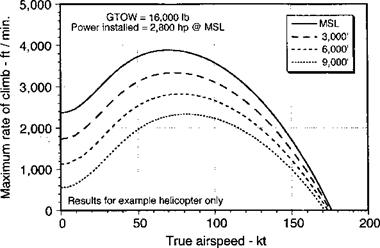
Figure 5.14 Maximum possible rate of climb as a function of airspeed for different density altitudes.

speed. The climb velocity can then be obtained from

= Pa-W + Po + Pp + Pm) = ДР

C J, ’ V У

where A P is the excess power available at that combination of airspeed and altitude.

Calculations of the maximum rate of climb as a function of flight speed and density altitude are shown in Fig. 5.14 for the example helicopter. These curves mimic the excess power available curves because the climb (or descent) velocity is determined simply by the excess (or decrease) in power required, A P, relative to steady level flight conditions. This excess is determined also by the power available from the engine (see next). Pilots often call the tendency of the helicopter to climb when translating from the hover condition as “translational lift.” However, the term is a misnomer because the helicopter climbs because of the excess power available and not because of any extra rotor lift. As shown by Fig. 5.14, the rate of climb performance is substantially affected by density altitude.