FURTHER ASSUMPTIONS

In the classical linear equations, m and g are constants, the vehicle is assumed to have a plane of symmetry, and the momenta of spinning rotors is excluded. The latter assumption is easily relaxed when rotor terms are important. As a particular choice for body axes we select Fs, the stability axes, for which a. Xf = we = 0 (see Sec. 4.2.7). Since the initial heading has no special significance in the flat-Earth approximation, we also set y>w = 0.

Instead of a. x, the angle of attack of the xs axis, we choose for the angle of attack variable that of the zero lift line (see Sec. 6.1). It is denoted simply a, and of course is not zero in the reference state, a and otx differ only by a constant in any particular ease.

In treating the thrust terms of (5.8,1) we wish to make allowance for rather general conditions, such as can occur in VTOL and STOL flight, when the thrust vector may be at large angles to the direction of motion. We therefore assume conditions as illustrated in Fig. 5.8. We further assume that the thrust vector rotates rigidly with the vehicle when it is perturbed. This implies that any rotation of the thrust relative to the vehicle is to be accounted for by adding suitable increments to L, D, and Y.

In the perturbed state, the thrust vector in body axes is

’ cos a. T ‘

TB = (Te + A T)

and in the wind axes is

Tjjr — LWBTB

On making use of (4.5,5) (with atx = Да therein) and linearizing, the result is

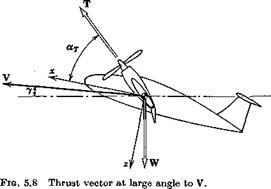TXw = (Te + AT) cos a. T — Aa. Te sin a. T (a) Tvw = – PTe cos aT (6)

TZW= — (Te + AT)sinct. T — Aa^cosay (c)

THE LINEAR EQUATIONS

In linearizing the appropriate members of (5.8,1) to (5.8,7), we assume that all the perturbation quantities AF, Да, p, etc., are small, and that squares and products of them may be neglected. It follows that cos Ау 1,

and sin Aу = Ay. Thus (5.8,1a) for example becomes

(Te + AT) cos a. T — ActTe sin аг — (De + AD) — mg sin (ye + Ay) = mt

or, on expanding the trigonometric term,

(Te cos xT — De — mg sin ye) + AT cos аг

— ДаTe sin ат — AD — mg cos уe Ay — mV

The part in brackets vanishes, since the reference state must satisfy the equations, and hence the final perturbation equation is

AT cos a. T — ДаTe sin olt — AD — mg cos ye Ay — mV (5.10,4)

Note that no approximation has been made here concerning ye. The equation applies to flight at any angle of climb or descent up to vertical flight. Pro­ceeding in a similar manner for all the other equations, the result is

AT cos а у — Да Te sin а у — AD — mg cos ye A у = mV		(a)
AY + mg cos уеф = m(v + Ver)	(b)
			(5.10,5)
AT sin а у + Аа Te cos а у + A L + mg sin	ye Ay = mVeqw		(o)
AT Ixp Tzxr	(a)
AM = Iyq	(&)		(5.10,6)
AN = Izr – Izxp	(c)
ф = p + r tan yt	, («)t
Y = 4w	Ф)		(5.10,7)
ip = r sec ye	(o)t
II 1			(5.10,8)
*E = Ve cos Ye + COS ye AV –	vesin Ye Ay	(a)
Уе = Ve COS ye ■ ip + V		(b)	(5.10,9)J
zE= – Fesinye – siny„AF-	– Ve cos ye Ay	(o)

Note that the order of the terms in (5.10,8) has been rearranged slightly as compared with (5.8,5) and that two of the latter are not needed. Of

(5.10,9) the first and third come from (5.8,6), and the second from (5.8,7).

Although the moment equations (5.10,6) were obtained by a linearization of (5.8,3), which are the equations for a rigid body, they are in fact valid for a deformable body. This is because the first term on the r. h.s. of (5.6,8) contains only the products of first-order rotations and rates of change of inertia coefficients. The latter are also first order in the linear model, and hence the distortional coupling terms are second order and negligible.

Because of the simplicity of the linear kinematical relations, it is convenient to eliminate qw and to regroup the equations as follows.

f Equations (5.10,7a – and c) cannot be regarded as a small-perturbation equation when ye —► ±90° for then <j> and ф -> oo for any finite r.

t Equations (5.10,9) are not strictly perturbation equations, albeit linear, because of the presence of the constant terms Ve cos ye and — Ve sin ye. The perturbations are strictly (xE – Ve cos ye), yE, and (zE + Ve sin ye).