LIFT CHARACTERISTICS OF PLAIN FLAPS

Ordinary or plain flaps are similar in shape to control flaps, elevators and/or rudders as described in Chapter IX.

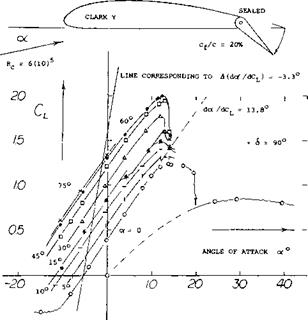
Lift Increment (aCl). Figure 2 presents the lift co­efficient of a flapped wing as a function of its angle of attack a as well as of the flap angle 6. The effect of the flap deflection is to displace the CL (o’ ) function by more or less a constant amount of ( a<x ). At constant lift coefficient, such ( aoC ) values can be considered to be independent of the wing aspect ratio. ‘The ratio (Aa1 /6) could thus be utilized to indicate the flap effectiveness. At the large deflection angles used during landing. Cu does not vary in linear proportion to the angle 6, however. A statistical evaluation is, therefore, needed. Using the angle-оf-attack displacement stated above, the lift due to flap deflection corresponds to aCu = daf (dCL/dot ), where the lift-curve slope (dCL/do( ) = 1 /(dot: /dCu) and the “lift angle” roughly:

Atf° /dCL * 10 + 20/A (6)

as discussed in Chapter III. To eliminate the second term (containing the aspect ratio A) that term is simply sub­tracted from the “lift angle” as tested. The result is a two-dimensional lift differential due to flap deflection, indicated by

(*CL) c* AcZ° /((doT° /dCL ) – (20/A)) (7)

A graphical procedure for the evaluation of this type of (ACi_) is indicated in figure 2,a. As discussed above, results from the modern “two-dimensional” closed wind – tunnel setups (2,c) have been “corrected” corresponding to A (dor’ /dCL ) = + 0.4°.

Figure. 2. Lift of a flapped rectangular model wing with A = 6, tested (10,a) in a closed wind tunnel:

Part a) as a function of the angle of attack of.

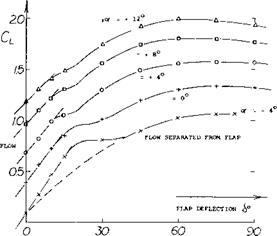
Part b) as a function of the flap angle 6.

(3) Summary and review of trailing-edge flaps:

a) Cahill; Data on Trailing-Edge Devices, with 58 references, with emphasis on slotted flaps; NACA TRpt 938 (1949).

b) Wenzinger, Summary as of 1939, SAE Journal 1939 p 161.

c) Serby, Review of Full-Scale Landing Flaps, ARC RM 1821 (1937).

d) Kruger, High Lift Devices, ZWB UM 3025 (1943) and Tech Berichte 1944 p 461.

e) See in Riegels, “Aerodynamische Profile”, Oldenbourg 1958.

f) Young, Characteristics of Flaps, ARC RM 2622 (1947), with 138 references (theory, flap types, pressure distribution, downwash, swept wings).

(4) NACA Investigation of Fairchild airplane in full-scale tunnel and in flight:

a) Dearborn, With Fowler Flaps, TN 578 (1936).

b) Dearborn, With Zap Flap and Ailerons, TN 596 (1937).

c) Reed, With External-Airfoil Flaps, TN 604 (1937).

d) Silverstein, Maximum Lift Without Flaps, NACA TRpt 618 (1938).

(5) Soule, Discussion of the Minimum Horizontal Tail Surface Required for Airplanes With Flaps; NACA TN 597 (1937).

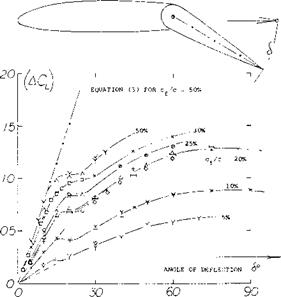
Flap Deflection. Values of (<dCL) are plotted in figure 3 as a function of the flap angle. As any plain-type flap is deflected from zero, its (aCl ) value increases first ac­cording to dot / S = f(cf /с). Between 6 := 10 and 20°

the flow will separate on the upper side of the airfoil. The actual flap angle for separation depends on the influence of Reynolds number, foil thickness ratio, flap-chord ratio, angle of attack “of ” and the size of the gap around the nose of the flap. After an interval in the order of 10°, the increment (ACl ) again increases, at a reduced and no longer linear rate, which is similar in character, to sin6. The increment (дСи) due to flaps usually reduces some­what as the angle of attack, or the basic lift coefficient is increased. We have generally evaluated flap effectiveness starting at oc =0, or at the angle of attack where the air­foil section used, see figure 2. At angles around 6 = 60°, the increment usually reaches a maximum. Any increase of the deflection angle above this limit, gives only a small increase of CL. For landing near CLX, for example a high angle of attack would becombined with a large flap angle. The increment (^CL ) will then be somewhat smaller than indicated in figure 3.

У	0009, Hor’tail,	50%,	6(10)5	(7, c)
v	0009, walls, 5 +	50%,	2(10)6	(7, d)
л	0009, walls, 25,	50%,	3(10)6	(7,e)
X	Cl-Y, A = 6, 10 +	30%,	6(10)5	(6, a)
□	64A010 wl’ 30%c	flap,	3(10)6	(7, f)
0	64A010, A = 3.1,	25%,	5(10)6	(23, e)
H	23012 bet’walls	20%,	3(10)6	(11,a)
Д	65-618, walls,	20%,	6(10)6	(9, a)
+	Clark Y, A = 6,	20%,	6(10)5	(6, a)
0	2412 with A= 5,	18%,	3(10)6	(6,b)
	23012 bet’walls	10%,	2(lO)6	(11, b)
	0009 with a 6%	tab,	2(10)6	(7,d)

— C. p

Figure 3. Lift increments (ACL ) in two-dimensional flow, of plain flaps deflected from conventional foil sections, at F^eynolds num­bers between 6(10)b~ and 6(10)6.

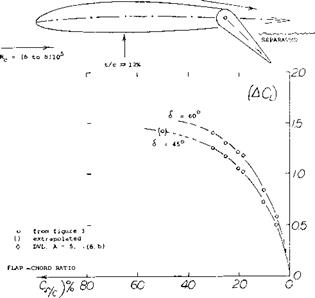
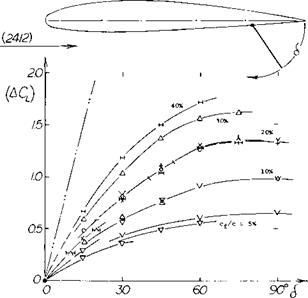
Flap-Chord Ratio. The effectiveness of plain flaps in­creases as a function of the cf /с ratio. As shown in figure 4, this increase is similar to

(4CL)~V^ (8)

Referred to the flap area indicated by the flap chord Cf effectiveness is highest in small chord ratios, and decreases rapidly as the ratio is increased. In the design of airplanes, chord ratios in the order of 20% for plain flaps have evidently been found to be most economical or practical, producing a comparatively large increment of lift with a limited structural penalty.

Figure 4. Lift increments of plain flaps (as in figure 3) as a function of their flap-chord ratio.

(6) Wind-tunnel investigation of simple wing flaps:

a) Wenziner, Ordinary and Split Flaps on Various Wings Having A = 6, at Rc = 6(10) NACA TRpt 554 (1936).

b) Bausch-Doetsch, Rectangular 2412 Wing With Flap and Tab in DVL Open-Jet Wind Tunnel, Yearbk D Lufo 1940 p 1-182.

(7) Investigations of plain control flaps:

a) Dods, Nine Related Straight and Swept Horizontal Tails, NACA TN 3497 (1955).

b) Bryant, Evaluation of Control-Flap Characteristics for Small Deflections, with 19 references; ARC RM 2730 (1955).

c) Gothert, Two Series of Airfoils With Flaps and Tabs Tested to 6 = 40° in Open-Jet Tunnel, Yearbk D Lufo 1940 p 1-542.

d) NACA, 0009 Foil Section Between Walls With 30,50, 80% Flaps and With Tabs, TNotes 759, 734, 761 (1939/1940).

e) Spearman, 0009 Section with 25 and 50% Control Flaps, NACA TN 1517 (1948).

f) Crane, 66-216 Airfoil With Flap and Tab, NACA TRpt 803 (1944).

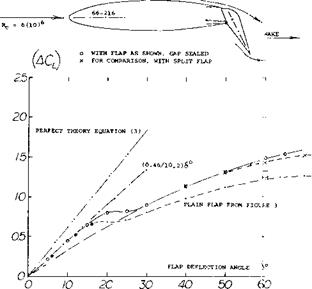
Figure 5. Lift increment of a plain flap (18,a) providing a well rounded shape when deflected.

Round Comer. With the larger radius made possible with the hinge located on the lower side as in figure 5, it would be expected that the flow would go further around the corner without separation than in a conventional plain flap, such as in figure 2 for example. Direct evidence for an improvement at deflections between 30 and 60 is not available. Two things can be seen however, in figure 5, the angle of incipient separation is raised from $ == 15 to 20°; and the lift increment (ACU ) keeps rising above b = 60°. Other factors contributing to the increase of lift over that of plain control-type flaps such as in figure 3, are:

a) the internal seal, preventing flow through the gap,

b) the thickness ratio t/c = 16%, in comparison to a 12%,

c) the 66-series section, in comparison to “old” shapes.

At any rate, the high effectiveness of the flap in figure 5 at larger angles of deflection is due to several factors as well as the greater radius.

(8) Influence of stream turbulence:

a) Abbott, 23012 Rectangular Wing With Plain and Split Flaps in the Variable-Density Tunnel, NACA TRpt 661

(1939) .

b) Morris, Flight Investigation Regarding the Effect of Vor­

tex Generators on Flap Effectiveness, NACA TN 3536 (1955). — 1

Stream Turbulence. The NACA’s Variable-Density Wind Tunnel is known to have a very turbulent stream of air, see Chapter IV. Results obtained for a 20% chord plain flap (8,a) are interesting in regard to the influence of turbulence upon the effectiveness of that type of flap. For <$=60 , the lift increment is:

(zlCL ) = 1.42 for the plain flap

= 1.27 for a same-size split flap

Comparison with the results in figure 3 shows that the lift is some 25% higher with plain flaps. The fact that the split flap does not exhibit an increased increment (see figure 6) proves that the phenomenon is not the result of tunnel interference. Thus, the conclusion is that stream turbu­lence helps the flow somewhat go around the bend of the plain flap. A reduction of turbulent separation, by way of “mixing” can also be produced by means of so-called turbulence generators small pieces of sheetmetal set at an angle of yaw on the upper side of wings, ahead of trailing – edge flaps. Flight tests (8,b) indicate the following:

a) Generators do not have a detectable effect at larger angles of flap deflection.

b) In climbing flight, with a flap angle of 19*, perform­ance is slightly improved.

H	23012,	WALLS,	20 +	40*,	3 <10)6	(10,b)
Д	23012,	WALLS,	10 +	30*,	3(10)6	(10,b)
Л	23012,	BET’WALLS,	20*,	3(10)6	(11 ,a)
+	23012,	WITH A	= 6,	20*,	8(10)6	(8, a)
X	23012,	WITH A	= 6,	20*,	6(10)5	(6, a)
	65-212	, BET WALLS	20*,	6(10)6	(10 / c)
о	0012, ‘	WITH A	= 6,	20*,	3(10)6	(10,a)
V	23012,	WALLS,	5 &	10*,	3(10)6	(15«,b)
V	AVA GOTTINGEN,	5,10,204	1932	(-10, f)

Figure 6. Lift increments (dC^) of split flaps deflected from conventional foil sections with t/c around 12%, at Reynolds num­bers between 6(10f and 6(10)6.