Luminescent Emission and Photodetector Response

After the luminescent molecules in PSP absorb the energy from the excitation light with a wavelength Лр they emit luminescence with a longer wavelength Л2 due to the Stokes shift. Luminescent radiative transfer in PSP is an absorbing- emitting process; the luminescent light rays from the luminescent molecules radiate in both the inward and outward directions.

For the luminescent emission toward the wall, the luminescent intensity I—

can be described by

where Sx (z) is the luminescent source term and the extinction coefficient Ph = єкc is a product of the molar absorptivity and luminescent molecule

concentration c. The luminescent source term Sx (z) is assumed to be

proportional to the extinction coefficient for the excitation light, the quantum yield, and the net excitation light flux filtered over a spectral range of absorption. Therefore, a model for the luminescent source term is expressed as

Sx 2(z) = Ф( p, T) Ex 2( X 2) £~ (q, 1 )net P, 1FJ X1 )dX, , (4.11)

where Ф( p, T) is the luminescent quantum yield that depends on air pressure (p) and temperature (T), Ex (X2) is the luminescent emission spectrum, and

Ft1( X1) is a filter function describing the optical filter used to insure the excitation light within the absorption spectrum of the luminescent molecules. With the boundary condition I— (z = h) = 0, the solution to Eq. (4.10) is

( -1 < И < 0 ) (4.12)

The incoming luminescent flux toward the wall at the surface (integrated over в = ж to ж/2 and в = ж to 3ж/2 ) is

Г0

q-2(z = 0) = -2 J ^ I-2(z = 0) И dp, (4.13)

where

1 eh Px 2Z

— I S x2(z)exp( )dz

p J0 2 p

We consider the luminescent emission in the outward direction and assume that the scattering occurs only at the wall. The outgoing luminescent intensity I + can

be described by

dl+

p~dzr + ^ I+2 = S2(z). (0 < p < 1) (4.14)

Similar to the boundary condition for the scattering excitation light, a fraction of the incoming luminescent flux q-2 (z = 0) is reflected diffusely from the wall. Thus, the boundary condition for Eq. (4.14) is

where pWp is the reflectivity of the wall-PSP interface for the luminescent light. The solution to Eq. (4.14) with the boundary condition Eq. (4.15) is

(-1 < p < 0) (4.16)

At this stage, the outgoing luminescent intensity I + can be readily calculated by substituting the source term Eq. (4.11) into Eq. (4.16). In general, I+ has a non­linear distribution across the PSP layer, which is composed of the exponentials of Px z and ph z. For simplicity of algebra, we consider an asymptotic but

important case — an optically thin PSP layer.

When the PSP layer is optically thin (px h, PX2h, px z and phz <<1), the

asymptotic expression for I + is simply

I+2(z) = Ф( p, T)qg Ex2(X2 )K 1 (Px/p)(z + 2ррр2 hp), (-1 < p <0) (4.17)

where

P-1 J~Px, Ex, a 1 )Cd(1 – p% )(1 + Pwp )FJІ1 ) dXx.

Eq. (4.17) indicates that for an optically thin PSP layer the outgoing luminescent intensity is proportional to the extinction coefficient (a product of the molar absorptivity and luminescent molecule concentration), paint layer thickness, quantum yield of the luminescent molecules, and incident excitation light flux. The term Kj represents the combined effect of the optical filter, excitation light scattering and direction of the incident excitation light. The outgoing luminescent intensity averaged over the layer is

h

<I+ >=h- A 2

where M( p) = 0.5 + 2pyp p. The outgoing luminescent energy flow rate Q+

(radiant flux) on an area element As of the PSP paint surface collected by a detector is

> cos в dQ = pXj h0( p, T )q0 EXi (A 2) Kj < M > As Q

(4.19)

where Q+ is equivalent to the spectral radiant flux in radiometry (watt-nm-1), Q is a collecting solid angle of the detector, and the extinction coefficient = ex c is a product of the molar absorptivity sx and luminescent molecule

concentration c. The coefficient < M > represents the effect of reflection and scattering of the luminescent light at the wall, which is defined as

< M > = Q – f M(p )dQ = 0.5 + pwp( + p2),

a 2

where = cos 61 and p2 = cos 62 are the cosines of two polar angles in the solid angle Q.

Imaging system aperture area, A0=ж D /4
Image of source area A
Source area A,
N ►
R

Fig. 4.3. Schematic of an imaging system

The response of a photodetector to the luminescent emission can be derived based on a model of an optical system (Holst 1998). Consider an optical system located at a distance R2 from a luminescent source area, as shown in Fig. 4.3. The collecting solid angle with which the lens is seen from the source can be approximated by Q ~ A0/R2, where A0 = ж D2/4 is the imaging system entrance aperture area, and D is the effective diameter of the aperture. Using Eq. (4.19) and additional relations As/R = A,/R2 and 1/R1 + 1/R2 = 1/fl, we obtain the radiative energy flux onto the detector

where F = fl / D is the f-number, M op = R2 / R1 is the optical magnification, fl

is the system’s effective focal length, A, is the image area, and Top and Tatm are

the system’s optical transmittance and atmospheric transmittance, respectively. The output of the detector is

V = G £~ Rq(l2 )(Q,2 )det Ft2( a2 №2 , (4.21)

where Rq(X2) is the detector’s quantum efficiency, G is the system’s gain, and Ft2 (X2) is a filter function describing the optical filter for the luminescent emission. The dimension of V/G is [V/G] = J/s. Substitution of Eq. (4.20) into Eq. (4.21) yields

A

V = G————- 1———- Д. h0(p, T )q0 K1 K2,

4 F2(1 + Mp)2 11 0 1 2

K2 = J~ Top Tam Exг(к2 )< M >Rq(X2 )FJX2 )dX2

The term K2 represents the combined effect of the optical filter, luminescent light scattering, and system response to the luminescent light. The above analysis is made based on an assumption that the radiation source is on the optical axis. In general, the off-axis effect is taken into account by multiplying a factor cos4 6p in the right-hand side of Eq. (4.22), where 9p is the angle between the optical axis

and light ray through the optical center (McCluney 1994).

Eq. (4.19) gives the directional dependency of the luminescent radiant flux

Q + – 1 + 2p’lp [cos(9-А9/2) + cos(9 + A9/2)] ,

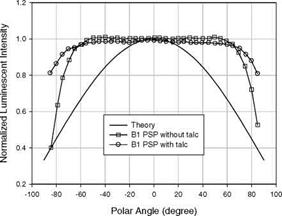
where Лв = в2 – в1 is the difference between two polar angles in the solid angle Q. Clearly, the luminescent radiant flux contains a constant irradiance term and a Lambertian term that is proportional to the cosine of the polar angle в. Le Sant (2001b) measured the directional dependency of the luminescent emission of the OPTROD’s B1 PSP composed of a derived Pyrene dye and a reference component. Figure 4.4 shows the normalized luminescent intensity as a function of the viewing polar angle for the B1 paint and the B1 paint with talc compared

with the theoretical distribution Eq. (4.23) with pJ = 0.5 and Лв = 4 degrees.

The experimental directional dependency remains nearly constant for both paints until the viewing polar angle is larger than 60o. The theoretical distribution for a non-scattering paint fails to predict the flatness of the experimental directional distributions of the luminescent emission. This is because the simplified theoreti­cal analysis does not consider scattering particles (e. g. talc and solid reference component particles) re-directing and re-distributing both the excitation light and luminescent light inside the paints. A more complete analysis of the radiative energy transport in a luminescent paint with scattering particles requires a numerical solution of an integro-differential equation (Modest 1993).

Fig. 4.4. Directional dependency of the luminescent emission from the B1 paint and B1 paint with talc, compared with the theoretical directional distribution for a non-scattering paint. Experimental data for the B1 paints are from Le Sant (2001b)