ORIENTATION OF THE AIRPLANE

We now need a set of differential equations from which the Euler angles can be cal­culated. These are obtained as follows: Let (i, j, k) be unit vectors, with subscripts 1, 2, 3 denoting directions (jc,, jq, z,), and so on of Fig. 4.2.

Let the airplane experience, in time At, an infinitesimal rotation from the position defined by ‘P, 0, Ф to that corresponding to (Ф + ДФ), (0 + Д0), (Ф + ДФ). The vector representing this rotation is approximately

Дп = i3 ДФ + j2 Д0 + ki ДФ

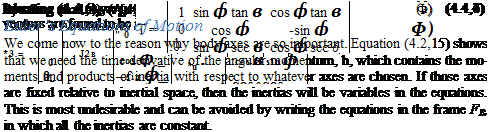and the angular velocity is exactly

We begin with the force equation of (4.2,15):

fE = mVf (4.5,1)

Both vectors in (4.5,1) are now expressed in FB components; thus:

UJ„ = m 4 (LBBVf) = m{tEBWEB + Y,:J’n) (4.5,2)

at

The derivative of the transformation matrix is obtained from (A.4) as

= L eb&b (4-5,3)

With (4.5,3), (4.5,2) becomes

LBBfB = mil, EgtO/jV B + LEBVB)

Now premultiply by LB/: to get

fB = m(Vf + шв%) (4.5,4)

A similar procedure applied to the moment equation of (4.2,15) leads to

GB hB + <wBhB (4.5,5)

The force vector f is the sum of the aerodynamic force A and the gravitational force mg, that is,

f = mg + A (4.5,6)

where

AB = [X Y Z]T

and

mgB = mhBEgE = mLB/. |0 0 gf (4.5,7)

We denote VB = [u’ vE vva 17 and use (4.3,26) for wB. Equations (4.5,4 and 5) are then expanded using (4.3,4) to yield the desired equations. In doing so we note that = [L M N]7 and l that, because the airplane is assumed to be rigid, Ів = 0. X — mg sin в = , m{tiE + qwE — rvE) (a) Y + mg cos в sin ф = m(vE + ruE -pwE) (b) (4.5,8) Z + mg cos в cos ф = m(wl ‘ + pvE – quE) (c) L = ~ “ Л АГ ~ r2) ~ IJr + pq) – – ш ■ – rp) – (Л – h)dr (a) M = I yd ~ – I Jr – P2) – hy(P + dr) – f;Jr – – Pd) – (Л – Qrp (b) (4.5,9) N = hf~ – IJP2 – d2) – IJd + rp) ■ ~ hIP – qr) – (Л – Iy)Pd (c)