Outline of the Analytical Method
1.1 Model Description
|
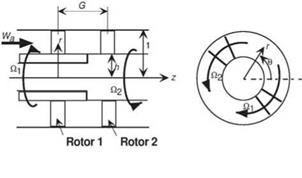
Figure 1. Contra-rotating annular cascades |
We consider a pair of annular cascades in an annular duct of infinite axial extent with the outer duct radius r** and the boss ratio h as shown in Figure 1. The undisturbed fbw is a uniform axial ft>w of axial velocity W *, static pressure p0 and fliid density p *. In the following unstarred symbols denote dimensionless quantities, where lengths, velocities, pressures and times are scaled with respect to r**, Wa*, p0 Wa*2 and r** /W*, respectively. Let subscripts 1 and 2 denote the upstream rotor 1 and the downstream rotor 2. Further following notations are used: NBі and NB2: numbers of blades, = H*rT*/Wa*(> 0,
clockwise looking from a downstream station) and H2(< 0, anti-clockwise): rotational angular velocities of the rotors, Ca1 and Ca2: axial chord length assumed constant along the span, (r, в, z), (r, в 1 ,z1) and (r, e2,z2): cylindrical coordinates fixed to the duct, rotor 1 and rotor 2 respectively. The angle coordinates and axial coordinates of different frames are related to each other by
в = в1 — Q1t = в2 — H2t, z = z1 = z2 + G. (1)
Here t denotes the time coordinate and G denotes the axial distance between the centers of rotor 1 and rotor 2.
We assume that the steady blade loading is zero, i. e., the time mean fbw is uniform, and that the unsteady disturbances induced by blade vibrations are small. Therefore the unsteady flow is governed by linearized equations.