Perturbation potential flows

We now assume irrotational flow. This allows eliminating the three u, v, w perturbation velocity components in terms of the single normalized perturbation potential variable ф, which is the usual perturbation potential p normalized with the freestream.

ф	= P/V2	(8.52)
u X + v y + w z	= Vф	(8.53)
V = Vo + V2(u x + v y + w z)	= V2 [(1 + фх) X + фу y + фz z]	(8.54)

Note that ф has units of length, so that Vф is dimensionless.

Second-order perturbation potential equation

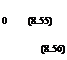Replacing u, v, w with фх, фу, фх in equations (8.49),(8.51) gives the Second-Order Perturbation Potential (PP2) equation and associated flow-tangency condition:

Transonic small-disturbance equation

We now note that for a small-disturbance flow, most of the quadratic terms in (8.55) can be dropped, except when the freestream flow is close to sonic, ~ 1. In this case we can approximate Q ~ y+1 , and we also note that Qфф. ~ (y + 1) фХ may not be small compared to (1 — ) фх. Furthermore, for slender bodies

we have

Пх ^ Пу j nz

so that the product фхпх in (8.56) is a higher-order quantity compared to фуny and фznz. Hence we drop all quadratic terms except for фХ, which results in the following nonlinear transonic small-disturbance (TSD) equation, and a first-order flow-tangency condition.

which looks like a Laplace equation except for the фх-dependent coefficient multiplying the фхх term.

Strictly speaking, the quadratic terms ф^ + ф2 in (8.56) should also have been retained in the TSD equa­tion (8.57). However, because of the strong lateral dilation effect shown in Figure 8.5 they are typically much smaller than QфХ and hence can be dropped. One possible exception is in cases with strongly swept shock waves, in which these may need to be retained.

Prandtl-Glauert equation

Provided the freestream flow is sufficiently far from sonic, we can in addition drop the quadratic term from the TSD equation (8.57) or (8.59) to give the Prandtl-Glauert (PG) equation.

The first-order flow-tangency condition (8.58) remains the same here. The most significant change from the TSD equation is that the PG equation is now linear, which is an enormous simplification which will be extensively exploited in the subsequent sections.

Laplace equation

As a final step, if we assume low speed flow, with M^ ^ 1, the PG equation (8.60) simplifies to the Laplace equation.

фхх + фуу + фzz = 0 (8.61)

Although this equation appears to be subject to the same small-disturbance approximations as its PG, TSD, and PP2 predecessors, it is in fact completely general for any low-speed flow. The reason is that all the higher-order terms which were dropped were also multiplied by M^ or higher powers, so that with M^ ~ 0 all these dropped terms were already negligible anyway. Alternatively, the Laplace equation could also have been obtained directly from the starting continuity equation (8.47) by a priori assuming that p is constant in the low speed case.