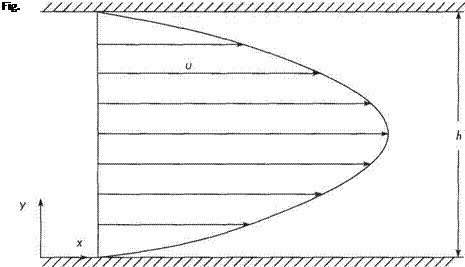
Plane Poiseuille flow – pressure-driven channel flow

This also corresponds to the flow between two infinite, plane, parallel surfaces (see Fig. 2.31). Unlike Couette flow, both surfaces are stationary and flow is produced by the application of pressure. Thus all the arguments used in Section 2.10.1 to simplify the Navier-Stokes equations still hold. The only difference is that the pressure term in Eqn (2.95a) is retained so that it simplifies to

“ё+’*|г=0 implyi, Ig “_^+Ciy+C2 <2108)

The no-slip condition implies that и = 0 at у = 0 and h, so Eqn (2.108) becomes

–ШО-0 (210,)

Thus the velocity profile is parabolic in shape.

The true Poiseuille flow is found in capillaries with round sections. A very similar solution can be found for this case in a similar way to Eqn (2.109) that again has
a parabolic velocity profile. From this solution, Poiseuille’s law can be derived linking the flow rate, Q, through a capillary of diameter d to the pressure gradient, namely

7rd4 dp 128/i dx

Poiseuille was a French physician who derived his law in 1841 in the course of his studies on blood flow. His law is the basis of another type of viscometer whereby the flow rate driven through a capillary by a known pressure difference is measured. The value of viscosity can be determined from this measurement by using Eqn (2.110).