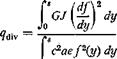SOLUTION BY GENERALIZED COORDINATES
An alternative procedure based on the semirigid assumption is to apply the concept of generalized coordinates. This point of view provides a new ground for refinements in the calculation.
Let us again consider the idealized problem of § 3.2. Assume that the angle of twist along the span is a known function of у with unspecified amplitude. Let us write
%) = 0of(y) (1)
* For a uniform beam, the angle of twist due to a concentrated torque applied at the tip (reference) section varies linearly along the span. So the assumption (Eq. 11) is consistent with the influence coefficients, and with the stiffness constant К given by Eq. 9.
|
|||
|
|||
|
|||
|
|
||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
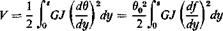
![]()
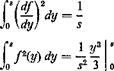
|
![]() 3 GJ c^aes1
3 GJ c^aes1
which agrees with the result in § 3.3.
Example 2. Let GJ, c, a, e be constants, and assume
,, , . -ny
|
|o/4s)rfs-{*in"f*/ = 5 |
AV) = sm —
Hence,
n4JJ
which agrees with the exact result. In the present approach, a correct assumption of the semirigid mode yields an exact solution.
The procedure can be generalized as follows: Let
П
%)в і Ш) о)
t = о
wheref({y) (/ = 0, 1, 2, • • •, n) are known functions, and are generalized coordinates. Then
Qi = ( Ma'(y)f№ dy И = 0, 1,2, • • ■, n)
Jo
At the critical-divergence speed,
(/ = 0, 1, 2, • • •, n) (9)
Equation 9 gives a set of homogeneous linear simultaneous equations in Since the вt are, by assumption, not all zero, the determinant of the coefficients of these equations must vanish. This determinantal equation
involves the dynamic pressure qd{v. Its real positive roots are the critical values.
In calculating the aerodynamic moment Ma’ in Eq. 8, a theory may be selected, such as Prandtl’s lifting-line theory or Weissinger’s theory. If we use the strip assumption, then
П
М: = qdh, c2ae^J), fiiy) (10)
1 = 0
Finally, let us remark that, if the functions f{(y) (i = 0, 1, 2, • • •) are infinite in number and form a complete set,* then in the limit n -> oo an exact solution can be obtained.!
Example. Let GJ, e, c, a be constants across the span, and assume
![]() %) = Яі – + Я2~-2
%) = Яі – + Я2~-2
S. Vs
Then
![]() + 26A + 022)
+ 26A + 022)
|
By strip theory, |
M; = q*ae (^ + 7**1) |
|
|
Hence, |
||
|
0i + —2 02) “ ty — qc^aes f (J70x + drl s / s Jo |
= ^aes (I + f)
Similarly,
Q2 = qc2aes
* A set of functions fjy), a < у < b, (i = 0, 1, 2, • • •) is said to be “complete” if an arbitrary function u{y) can be expanded into a generalized “Fourier” series of the
OO
formic,/to). i=o
t If the function fly) in Eq. 1 is regarded as unknown, the equation governing/(2/) can be derived from Eq. 5 by considering the first variation of that equation with respect to f(y). The result is the same as that obtained in § 3.2.
|
1 = GJ^aec2si
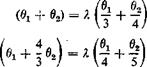 |
Then the equations of equilibrium 9 become
A nontrivial solution exists only if the determinantal equation
is satisfied. The two roots are X = 2.48 and 32.3, corresponding to
2.48 G/ 32.3GJ
—– гт and ———-
The first one is the “fundamental” divergence dynamic pressure. Compared with the exact value given by Eq. 17 of § 3.2, the error is 0.6 per cent too large.