Speed for Minimum Power
On the basis of the preceding analysis, it is clear that many of the performance characteristics of the helicopter in forward flight may be estimated directly from curves of excess power available and fuel bum relative to that required for straight-and-level flight at the same airspeed. For example, the maximum possible rate of climb is obtained at the speed for minimum power in level flight (this speed is often denoted by or Vy). It can be seen from Fig. 5.11 or Fig. 5.12 that this situation occurs at a fairly low airspeed, usually in the range 60-80 kts.
The speed Vmp will also be the optimum speed to fly for minimum autorotative rate of descent. At this airspeed the power required by the rotor is a minimum, and for an autorotation at this airspeed the pilot will need to give up the least amount of potential energy (altitude) per unit time. Thus, on the basis of the form of the power required curve it can be deduced that in the event of a mechanical failure in the hover condition, it is beneficial for the pilot to translate some of the stored potential energy into translational (forward flight) kinetic energy because the autorotative rate of descent under these conditions will be lower. However, if a mechanical failure occurs close to the ground, this transition may not be possible. For this reason, the normal operational envelope of a helicopter is restricted to an acceptable combination of altitude and airspeed that always allows safe autorotational landings to be performed (see Section 5.6.1).
In addition to being the speed to fly for maximum rate of climb and minimum autorotative rate of descent, Vmp also determines the speed to give the best endurance, that is, to obtain maximum loiter time on station for surveillance, search, and so on. To obtain maximum endurance the fuel bum per unit time must be a minimum. Now, the weight of fuel burned Wf in a given time t is given in terms of SFC (lb hp-1 hr-1) as
![]()
![]() WF = SFC x Pt,
WF = SFC x Pt,
so the endurance (in appropriate units) for a given amount of fuel is
WF
SFC x P’
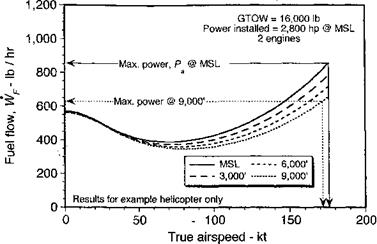
Clearly this time is maximized at the best SFC and lowest power required for flight. Figure 5.16 shows representative fuel bum curves for the example helicopter. Because the engine SFC curve is fairly flat over the range of power settings where engines will operate in practice (Fig. 5.15), the fuel bum is proportional to power at a given pressure altitude and temperature, and the speed for minimum fuel bum coincides with the speed for minimum
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
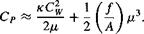
![]()

Note that, in general, this speed will increase with increasing density altitude, that is, with both increases in altitude and temperature. In addition, it will be apparent that this airspeed is proportional to the square-root of disk loading and helicopter weight.