STEADY STATES

It is of interest to deduce from the preceding general equations what “equilibrium points” exist for a flight vehicle. Neglecting motion of the Earth center, a true state of rest in inertial space occurs only when the vehicle travels due west at a rate exactly equal to that of the local eastward motion of the Earth. This is too restricted a case to be useful. Equilibrium in a more general dynamical sense corresponds to equilibrium of all the external forces, i. e. a state of zero acceleration, or rectilinear motion. On a round Earth, this kind of equilibrium is also not useful, since the flight path would then either intersect the Earth, or go off into space. The useful definition is that of an “aerodynamic steady state,” in which the motion, the aero­dynamic field, and gravity are all constant in the frame FB. Thus the aero­dynamic pressure distribution and the gravity components are constant with time. Such a state requires, first, that (u, v, w) or (F, otx, fl) and the rates of rotation (со — a>E)B of FB relative to the atmosphere or to FE be constants. Second, the Euler angles в, <j> that affect the gravity components must be constant. Constancy of aerodynamic forces at constant (V, ax, /1) also re­quires constant air density, i. e. constant altitude flight. Thus 0W = 0. Now consider the force equation (5.6,2). By postulate, the derivative terms are zero, and the left-hand side is constant. It follows that these equations can be solved for the constant values of

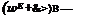P B+P йХв + Я rEB + r_

Since the sum and difference (line 14 above) of ыЕв and <aB are constants, then they must be separately constant. Since (a, fl) and (p, q, r) are constants, then from (5.2,13), (pw, qw, rw) are also constant, and transforming the constant ыЕв into Fw leads to a constant <aBw. Now the components of шЕ can be constant in Fw and/or FB, with the constraint of constant altitude, only if the motion of the frame is a rigid-body rotation around the Earth’s axis. Thus the path of the vehicle mass center must be a circle around the axis, i. e. it must be a minor circle of the Earth, lying on a parallel of latitude. Analyti­cally this means that X = const, and y> = ±7t/2. The conditions for this most general steady state may then be summarized as follows, taking the

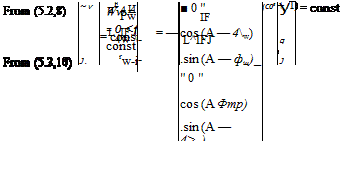The wind-axis force equations (5.5,8) then reduce to

TVw — G + mg sin </>w = —mV sin (A — ^TF)(2coE + /і) (5.9,6)

TZw — L+ mg cos <j>w = mV cos (A — </>w)(2coE + /і)

The reduced moment equations for this case are of little interest, since they contain only second-degree terms in (p, q, r), and the latter are clearly of order (ooE + ft), which is at most about 10~3 rad/sec for suborbital flight. They therefore reduce to L = M = N = 0.

To be exact, even this restricted steady state cannot exist, for the following reasons:

(i) All real vehicles in horizontal flight have propulsion systems that utilize fuel, so m is never strictly constant.

(ii) The Earth is not a perfect sphere, so that flight at constant altitude (i. e. air density) is not strictly flight on a circle.

(iii) The atmospheric density is never exactly constant and the wind never exactly zero at a given height.

These deviations from the idealized steady state are, of course, not im­portant enough to invalidate its usefulness.

If the Earth rotation ыЕ can be neglected, then clearly no one minor circle is preferable to any other, and the steady state can be on any minor circle over the Earth. In the flat-Earth approximation, the minor circle becomes any circle parallel to the ground surface. If in addition the variation of p with height can be neglected, as for a shallow climb or glide, the most general steady state becomes a vertical helix, i. e. a climbing or gliding turn.