SUPERPOSITION OF SOURCES AND FREE STREAM: RANKINE’S OVAL

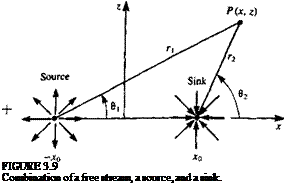
As a first example for using the principle of superposition, consider the two-dimensional flow resulting from superimposing a source with a strength a at x = —Xq, a sink with a strength —a at x = +x0- both on the * axis, and a free stream flow with speed Um in the x direction (Fig. 3.9). The velocity potential

for this case will be

Ф(дс, z) = Ikx + ^ In (rO – ~ In (r2) (3.87)

where і"і = V(* + x0)2 + z2, and r2 = VC* — x0)* + z2. The stream function can be obtained by adding the stream functions of the individual elements:

Ф(х, z) = U„z + ^ 0! – ^ в2 (3.88)

where

Z Z

в і = tan-1——– and 02 = tan-1——————-

X +x0 x – x0

Substituting rt, r2, ви and в2 into the velocity potential and the stream function yields

Ф(х, z) = Uojc + ~~In V(x + x())2 + z2-In V(x – x0)2 + z2 (3.87a) 2n 2n

The velocity field due to this potential is obtained by differentiating either the velocity potential or the stream function:

ЭФ ri, о x+xo a x-x„

и = — = t4 + —- ——- -5—– — ——— rx— 5 (3.89)

Эх 2л (x + x0)2 + z2 2л (x – x0)2 + z2

ЭФ о z о z

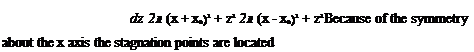W = — = — -—:———ї ~ :———— гт“—5 (3.90)

along the x axis, at points further out than the location of the source and sink, say at x = ±a (Fig. 3.10a). The w component of the velocity at these points (and along the x axis) is automatically zero, too. The distance a is then found by setting the и component of the velocity to zero

and a is

(3.91)

Consider the stagnation streamline (which passes through the stagnation

4′(*,z) = l/„z+-3tan l—TT-Tl^n l~_x ZJT X T Xq £7% X Xq

points). The value of Ф for the stagnation streamline can be found by observing the value of Eq. (3.88) on the left-side stagnation point (where 6y = 62 = я, and z = 0). This results in V = 0, which can be shown to be the same for the right-side stagnation point as well (where = 62 = 0). The equation for the stagnation streamline is therefore

The streamlines of this flow, including the stagnation streamline, are sketched in Fig. 3.10a and the resulting velocity distribution in Fig. 3.10b. Note that the stagnation streamline includes a closed oval shape (called Rankine’s oval after W. J. M. Rankine, a Scottish engineer who lived in the nineteenth century) and the x axis (excluding the segment between x = ±a). This flow (source and sink) can therefore be considered to model the flow past an oval of length 2a. (For this application, the streamlines inside the oval have no physical significance.) The flow past a family of such ovals can be derived by varying the parameters a and x0 or a, and by plotting the corresponding streamlines.