Synthetic Turbulence Generation Methods (STGM)

In this study, the identification of flow regions where RANS should be replaced by a higher order turbulence model represents the first step for the zonal approach. The second step is the proper coupling of RANS and LES flow domains. In order to keep overlapping regions of both computational domains as small as possible, effective mechanisms for turbulence generation have to be applied in LES inflow regions. The turbulent intensities coming from the RANS domain are introduced first at the LES inflow plane via synthetic turbulent eddies (Jarrin et al. [12], Batten et al. [2]) and controlled further downstream by employing control planes according to Spille and Kaltenbach [24]. The synthetic turbulence generation methods of Jarrin et al. and Batten et al. were implemented and tested for incompressible and compressible flows.

Method of Jarrin et al.

The method of Jarrin et al. [12], called synthetic eddy method (SEM), is based on the considering of turbulence as a superposition of coherent structures. These structures are generated over the LES inlet plane and are defined by a shape function which describes the spatial and temporal characteristics of the turbulent structure.

The shape function fa that has a compact support on [-a, a] where a is a length scale which satisfies the normalization condition

Table 1 Suggested critical and reference Values for three different flow types – Oblique shock at flat plate Transonic profile flow Subsonic profile flow c f, re f 0.002 0.004 0.004 ftref 1 1 1 cf, crit 0.0001 0.0001 0.0001 Pcrit 4 4 4

where A defines the extent of the domain. A one component velocity signal can then be described by the sum of the contribution u(i)(x) of a turbulent spot i to the velocity field. Let N be the number of prescribed synthetic eddy cores at the inlet and ei is a random number within the interval from — 1 to +1 then the one-dimensional velocity fluctuation component reads

(4)

The generalization of the one-dimensional procedure to time dependent two-dim­ensional fluctuations is straight forward.

Turbulent length and time scales are determined by the Reynolds shear stress component (u’v’) and the turbulent viscosity vt; both are extracted from corres­ponding RANS simulations. In this work, the Spalart-Allmaras turbulence model [23] was used for the incoming RANS solution. The turbulent time scale can be written as t = к/є and the turbulent length scale as L = t Vb with Vb = Vk where к and є stand for the turbulent kinetic energy and turbulent dissipation, respectively. By applying the experimental correlation of Bradshaw et al. the turbulent kinetic energy is related to the Reynolds shear stress (u’v1) and the turbulent viscosity vt which is available from the RANS solution

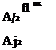| — (u’v’)| = Vt

with fli = уґсЦ and = 0.09. The turbulent dissipation є is approximated by the definition of the eddy viscosity from the k — є turbulence model (Menter [20])

The final flow field at the inlet is constructed from the resulting vortex field of Eq. 4

ill — Hi I иijiij (7)

where aij is computed from the prescribed Reynolds stress tensor applying a Cholesky decomposition.

Method of Batten et al.

The second method was introduced by Batten et al. [2] based on the work of Smirnov [21] and initially developed by Kraichnan [16]. To create a three-dimen­sional, unsteady velocity field at the inflow plane of the LES region, velocity com­ponents are constructed using a sum of sines and cosines with random phases and amplitudes. The intermediate velocity, vi, reads

Vj(xj. t) = — jr [p" cosd’j fj + cont + q" sind’jfj + cont],

n=1

where X are spatial coordinates being normalized by turbulent length – and time scales. These scales are reconstructed from the incoming RANS solution via Eqs. 5 and 7. The amplitudes of the signal are calculated by

pn = EijkZjdl, qn = £l}k^jdkk (9)

where | and Z are equal to N (0,1) and dn = dnV/cn. The wave number d, n = N (0,0.5) is elongated by the following relation according to Batten [2]:

In Eq. 8 the random frequencies con are taken from the normal distribution N (1,1). Like in the method of Jarrin et al. the synthetic turbulent fluctuation field is fi­nally reconstructed using the Cholesky decomposition. The methods are suitable in incompressible flows. In compressible flows, however, the velocity fluctuations are coupled with the density field. Thus, Morkovin’s hypothesis is applied to relate density and velocity fluctuations by assuming that the pressure fluctuations over the inflow plane are negligible

^ = (y-l)M2- . (11)

p u