The Added Mass

In situations when a body is accelerated in a fluid, it is possible to use Newton’s second law, in its most simple form, to compute the force F acting on the body. For example, if the body motion is parallel to the 2-axis then:

Of course the mass mto, consists of the mass of the body m, and of the fluid m’ that is being accelerated as well. Unfortunately, the evaluation of the added mass (m’) is not always easy since in most situations the local fluid acceleration may be caused by effects other than the body’s motion (e. g., in the case of a time-dependent wake-induced downwash). But in the case of a constant acceleration of a flat plate normal to itself, in a fluid at rest, the added mass can be more easily evaluated (see also Section 8.2.3).

Consider the flat plate of Fig. 13.12 accelerating in a fluid, such that the acceleration w is constant (see also Fig. 8.24). Since the continuity equation is independent of time, at each frozen moment the potential will be similar to the steady-state flow potential of the flow normal to the plate. From Section 6.5.3 the potential for such a flow is

(13.38)

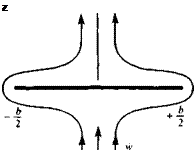where + is used for the potential above the plate and – is used for the potential below it. This is an elliptic distribution of the potential, similar to the

FIGURE 13.13

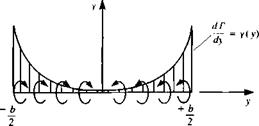Spanwise circulation on a flat plate in a sinking motion.

one obtained in Chapter 8 for the lifting-line and slender-wing theories. Because of the antisymmetry between the upper and lower surfaces,

АФ(З’) = 2Ф+(у) = wb yjl – (13-39)

It is interesting to point out that АФ in this equation can be replaced by Г and its derivative is the spanwise circulation y(y) as shown in Fig. 13.13. Examining the terms in the pressure equation (Eq. (13.23)) reveals that for this motion (V0 + S2 X r) • V4> = (0,0, w) • УФ = 0 since УФ will have a у component only, on the plate’s surface. (This can be deduced from Fig. 13.13, too, by observing that the “traditional” lift уx (0,0, w) has no vertical component.) Therefore, the pressure difference is due to the velocity potential’s time derivative дФ/dt, only, in the unsteady Bernoulli equation, and is

The integral is easily evaluated by recalling that the area of the ellipse is жЬ/4 and the lift L’ of a massless plate becomes

Note that because of the left/right symmetry, the center of pressure is at у = 0. Also, the lift is created only if the plate is under acceleration and the amount of fluid being accelerated (added mass) is equal to the mass of a fluid cylinder with a diameter of b {m’ — рЬ2(ж/4)), and in summary we can write

L’ = m’w (13.41a)