The equipotential

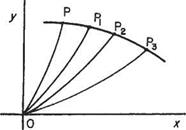
Consider a point P having a velocity potential ф (ф is the integral of the flow component along OP) and let another point Pi close to P have the same velocity potential ф. This then means that the integral of flow along OPi equals the integral of flow along OP (Fig. 3.3). But by definition OPPi is another path of integration from О to Pi. Therefore

Fig. 3.3 but since the integral along OP equals that along OPi there can be no flow along the remaining portions of the path of the third integral, that is along PP^ Similarly for other points such as P2, P3, having the same velocity potential, there can be no flow along the line joining Pj to P2.

The line joining P, Pi, P2, P3 is a line joining points having the same velocity potential and is called an equipotential or a line of constant velocity potential, i. e. a line of constant ф. The significant characteristic of an equipotential is that there is no flow along such a line. Notice the correspondence between an equipotential and a streamline that is a line across which there is no flow.

The flow in the region of points P and Pi should be investigated more closely. From the above there can be no flow along the line PPb but there is fluid flowing in this region so it must be flowing in such a way that there is no component of velocity in the direction PPi. So the flow can only be at right-angles to PPb that is the flow in the region PPi must be normal to PPi. Now the streamline in this region, the line to which the flow is tangential, must also be at right-angles to PPi which is itself the local equipotential.

This relation applies at all points in a homogeneous continuous fluid and can be stated thus: streamlines and equipotentials meet orthogonally, i. e. always at right – angles. It follows from this statement that for a given streamline pattern there is a unique equipotential pattern for which the equipotentials are everywhere normal to the streamlines.