THE FORCE VECTOR

The force vector for atmospheric flight consists of two parts, the aero­dynamic reaction (including propulsive force) A, and the weight mg, i. e.

f = A + mg (5.5,3)

In the wind-axis system Fw, the components of A are given by

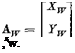(5.5,4)

It is convenient further to subdivide A into the “configuration aero­dynamics” and the propulsive force thus

	‘D’		—– j *
Aw — —	G	+	T vw
	_L_		T L-1 zwJ

Where D is drag, G is side force, and L is lift. The directions of D, C, L relative to the vehicle are illustrated in Figs. 4.4 to 4.6. The separation of the thrust from the other forces is to some extent always arbitrary, but is nevertheless useful. Any of the components of T may be large when we consider the flight of rockets or of V/STOL aircraft, although in the cruising flight of airplanes only Tx is usually significant. Finally the gravity force is given by

ГОП

In terms of the wind-axes Euler anglesf this becomes, from (4.5,4)

—sin 0,

mgw mg cos 0W sin <j>w

cos Bw cos <j>w so that the expanded set of scalar equations is

TXw — D — mg sin 6W = mf (a)

TVw — C + mg cos вw sin <j>w = mV(rEw + rw) (b) (5.5,8)

TZw — L + mg cos dw cos <f>w = —mV(qEw + qw) (c)

The terms rBw and qEw will vanish when Earth rotation is negligible.

The above equations are most conveniently regarded as having the primary dependent variables F, rw, qw. However they are not complete in the sense that the aerodynamic and thrust forces contained in them are functions not only of the above three variables, but also of pw, and of the aerodynamic angles a and /? (see Sec. 4.3). The moment equations and some additional kinematic relations must be used to complete the mathematical system; these are presented in the following sections. Little use has been found for

f The elements of LWy, i. e. the direction cosines of Fjy, can be used as the orientation unknowns instead of the Euler angles, see Sec. 5.2.

the moment equations in the Fw frame, and these are given below only for FB.