The velocity potential

The stream function (see Section 2.5) at a point has been defined as the quantity of fluid moving across some convenient imaginary line in the flow pattern, and lines of constant stream function (amount of flow or flux) may be plotted to give a picture of the flow pattern (see Section 2.5). Another mathematical definition, giving a different pattern of curves, can be obtained for the same flow system. In this case an expression giving the amount of flow along the convenient imaginary line is found.

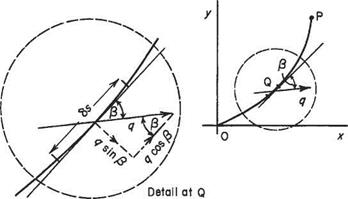
In a general two-dimensional fluid flow, consider any (imaginary) line OP joining the origin of a pair of axes to the point P(jc, y). Again, the axes and this line do not impede the flow, and are used only to form a reference datum. At a point Q on the line let the local velocity q meet the line OP in /3 (Fig. 3.1). Then the component of velocity parallel to 8s is q cos /3. The amount of fluid flowing along 8s is q cos /3 8s. The total amount of fluid flowing along the line towards P is the sum of all such amounts and is given mathematically as the integral f q cos /3 ds. This function is called the velocity potential of P with respect to О and is denoted by ф.

Now OQP can be any line between О and P and a necessary condition for Jq cos /3dy to be the velocity potential ф is that the value of ф is unique for the point P, irrespective of the path of integration. Then:

(3.1)

If this were not the case, and integrating the tangential flow component from О to P via A (Fig. 3.2) did not produce the same magnitude of ф as integrating from О to P

Fig. 3.1

Fig. 3.2

via some other path such as B, there would be some flow components circulating in the circuit OAPBO. This in turn would imply that the fluid within the circuit possessed vorticity. The existence of a velocity potential must therefore imply zero vorticity in the flow, or in other words, a flow without circulation (see Section 2.7.7), i. e. an irrotational flow. Such flows are also called potential flows.

Sign convention for velocity potential

The tangential flow along a curve is the product of the local velocity component and the elementary length of the curve. Now, if the velocity component is in the direction of integration, it is considered a positive increment of the velocity potential.