Thin Shear Layer Navier-Stokes Equations

In the open form of Navier-Stokes equations (2.53), we observe the existence of second derivatives for the velocity and the temperature. This implies that the Navier-Stokes equations are second order partial differential equations. When the freestream speed is high, the Reynolds number is high. This makes the gradients of the flow parameters to be high normal to the surface as compared to the gradients parallel to the surface. Therefore, we can neglect the effect of the viscous terms which are parallel to the flow surface and simplify Eq. 2.53. Let us now, perform some order of magnitude analysis for the simplification process on a simple wing surface immersed in a high free stream speed given in Fig. 2.7.

Since we consider the air flowing over the wing as a real gas, the boundary conditions on the surface will be (i) no slip condition and (ii) the wall temperature specification. According to Fig. 2.7, the wing surface is almost parallel to xy plane where the molecular diffusion parallel to the xy plane is negligible compared to the diffusion taking place normal to the surface. This is because of high free stream speed transporting the properties in the parallel direction much faster than the molecular diffusion. On the other hand, because of no slip condition, the gradients which are normal to the surface are much higher than the gradients parallel to the surface. The order of magnitude analysis performed on the terms of Eq. 2.53 gives

The approximate form of the equations result in modeling an external real gas flow which takes place in a thin shear layer around the wing surface. Therefore, the first approximate form of Eq. 2.53 is called ‘Thin Shear Layer Navier-Stokes Equations’ which are to be introduced next

Fig. 2.7 Thin wing in a high freestream speed

Eq. 2.54 are written in Cartesian coordinates without considering the wing thickness effect. If we consider the thickness effect and high angles of attack, Eq. 2.54 can be written in coordinates where only the viscous terms in f coordinate, which is normal to the wing surface are retained. With these assumptions and furthermore if we assume that the general coordinate system changes with time, the transformation of coordinates from Cartesian to generalized reads

n = <(x, y, z, t) , y = y(x, y, z, t) , f = f(x, y, z, t) , s = t (2.55)

Using 2.55, we can write the open form of the non-dimensional Thin Shear Layer Navier-Stokes equations in generalized coordinates where 1 is the direction normal to the wing surface

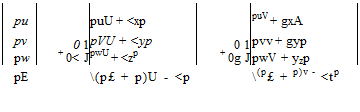
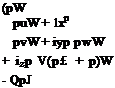
0 1

01J

1 0S

Re 01

Here, J = 00((<X’ y’ z ’S)1 is the Jakobian determinant of the transformation, U, V and W are the contravariant velocity components which are normal to the curvilinear surfaces given with constant <, y and 1 coordinates, respectively. They read

In curvilinear coordinates, we neglect the 0()/0t terms as well as the time dependency of П, g and f coordinates. Thus, we obtain the parabolized Navier – Stokes equations in curvilinear coordinates. In addition if we can, somehow, impose the pressure from the outside of shear layer then we obtain the well known boundary layer equations.