To find the stream function у/ of a source

Place the source for convenience at the origin of a system of axes, to which the point P has ordinates (x, _y) and (r, 9) (Fig. 3.6). Putting the line along the. v-axis as ф = 0

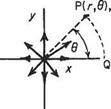
Fig. 3.6

(a datum) and taking the most convenient contour for integration as OQP where QP is an arc of a circle of radius r,

ф = flow across OQ + flow across QP = velocity across OQ x OQ + velocity across QP x QP

„ m „
: 0 + -— x гв
2-кг

Therefore

or putting в = tan 1 (y/x)

, m і У ф = — tan“- 2t x

There is a limitation to the size of в here, в can have values only between 0 and 2n. For ф = тв/2тг where в is greater Ijhan 2tt would mean that ф, i. e. the amount of fluid flowing, was greater than m m2 s, which is impossible since m is the capacity of the source and integrating a circuit round and round a source will not increase its strength. Therefore 0 < 9 < 27Г.

For a sink

ф = —(т/2-к)в

To find the velocity potential ф of a source

The velocity everywhere in the field is radial, i. e. the velocity at any point P(r, в) is given by q = л/q + q and q = qn here, since qt = 0. Integrating round OQP where Q is point (r, 0)

ф= qcosf3ds+ qcos/3ds

Joq JQP

= / qndr+ [ qtr89 = [ qndr + 0 Joq Jqp Joq

But

m

2irr

Therefore

fm m r

ф= I -—dr = —In— Jro 2-їїг 2n r0

where ro is the radius of the equipotential ф = 0.

Alternatively, since the velocity q is always radial (q = qn) it must be some function of r only and the tangential component is zero. Now

m дф

Therefore

(3.7)

In Cartesian coordinates with ф = 0 on the curve го = 1

ф = £1п^+ЇЇ

The equipotential pattern is given by ф = constant. From Eqn (3.7)

, m, ^ m,

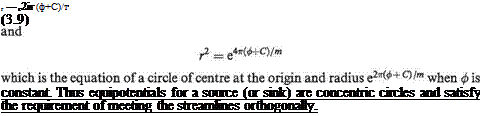ф = — In r — C where C = — lnro