Tragfliigeltheorie nach der Methode der Wirbelbelegung

7.21 Wirbelsystem der tragenden Flache

In Кар. 7.1 war der Einfachheit halber angenommen worden, daB die den Tragfliigel darstellende Zirkulation auf einer Linie kon – zentriert ist (Traglinientheorie), Abb. 7.2. Diese Vorstellung ist nur dann eine einigermaBen gute Annaherung fiir einen wirklichen Tragfliigel, wenn seine Tiefenerstreckung sehr viel kleiner ist als seine Spann­weite nerstreckung (Tragfliigel von groBem Seitenverhaltnis). Ist die Fliigeltiefe nicht mehr sehr viel kleiner als die Spannweite, so muB man von der Vorstellung der Traglinie zu derjenigen einer flachenhaften Verteilung der tragenden Wirbel iiber die Fliigeltiefe iibergehen. Eine solche kontinuierliche Wirbelverteilung iiber die Fliigeltiefe war bereits in Кар. 6.32 bei der Skelett-Theorie zugrunde gelegt worden. Im vorigen Abschnitt waren die freien Wirbel bereits flachenhaft verteilt ange­nommen worden. Ubertragt man diese Vorstellung der kontinuier – lichen Zirkulationsverteilung sinngemaB auf den Tragfliigel endlicher Spannweite, so ergibt sich fiir diesen eine in Tiefen – und Spannweiten – richtung veranderliche flachenhafte Wirbelverteilung (Tragfldchen – theorie). Diese Tragflachentheorie soil im vorliegenden Abschnitt in ihren Grundziigen entwickelt werden. Sie ist praktisch besonders wichtig fiir Tragfliigel von kleinem Seitenverhaltnis, fiir Pfeilfliigel und Delta – fliigel so wie fiir den schiebenden Fliigel.

Diese flachenhafte Wirbelbelegung kann aufgefaBt werden als eine Singularitatenbelegung im Sinne von Кар. 6.32. In der spateren Ent – wicklung der Tragflachentheorie wird anstelle der Wirbelbelegung ge – legenthch auch eine Dipolbelegung verwendet, vgl. z. B. L. Prandtl

[63] .

Die Tragflachentheorie mit Hilfe der Wirbelbelegung ist im AnschluB an die bekannte Prandtlsche Arbeit [61] zuerst von H. Blenk [4] weiter ausgebaut worden, indem er die Birnbaum-Ackermannsche Theorie [3] vom ebenen Fall auf den raumlichen Fall tibertrug.

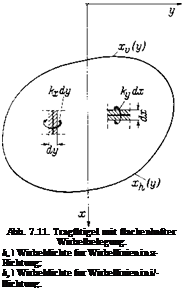Die Verteilung der Wirbelstarke iiber eine vorgegebene Flache kann in verschiedener Weise erfolgen. Es sei eine Tragfltigelflache von beliebiger Gestalt vorgegeben. Wir wahlen ein rechtwinkliges, fltigelfestes Koordi- natensystem so, daB die y-Achse senkrecht zur Anstromrichtung steht.

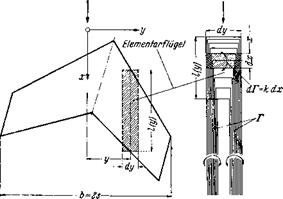
Eine erste Moglichkeit, diesen Trag – fliigel durch eine Wirbelbelegung zu ersetzen, besteht darin, daB diese Flache mit zwei flachenhaften Wirbel – verteilungen kx(x, y) und ky(pc, у) be – legt wird, Abb. 7.11. Die erstere Wirbelverteilung hat Wirbellinien parallel zur a;-Achse und die letztere solche parallel zur y-Achse. Die ky- Wirbel sind von der Art, wie sie bereits bei der ebenen Tragfltigel­theorie, vgl. Abb. 6.14, zugrunde ge – legt wurden, wahrend die AvWirbel von der Art der freien Wirbel in der Wirbelflache hinter der Tragflache

sind, vgl. Abb. 7.5. Bei Anstromung in a;-Richtung bringen ftir den Auftrieb der Tragflache nur die A^-Wirbel einen Beitrag. Die Gesamt – zirkulation ftir einen Fltigelschnitt у betragt

4

Г(у) = j kv(x, y) dx.

Hierin bedeuten xv(y) und xh(y) die a;-Koordinaten der Vorder – bzw. Hinterkante des Schnittes y. Die Wahl der beiden Wirbelverteilungen kx(x, y) und ky(x, y) kann nicht willktirlich sein, sondern muB so be – stimmt werden, daB die von der Wirbelflache induzierten Geschwindig – keiten die Gleichung der Drehungsfreiheit du/dy — dv/dx = 0 erftillen, Gl. (2.32). Entsprechend Gl. (6.60a) ist in der Nahe der Wirbelschicht (z -> 0):

и = ih ky, v = – p kx, (7.34)

2 Schlichting/Truckenbrodt, Aerodynamik, Bd. II, 2. Aufl.

wobei die oberen Vorzeichen oberhalb und die unteren Vorzeichen unterhalb der Wirbelschicht gelten. Mithin folgt dann:

= 0.

Man nennt diese Beziehung auch die Bedingung der Quellfreiheit der Wirbelbelegung. Da nach Gl. (2.135) kx ~ cox und ky ~ a)y ist, kann man die vorstehende Gleichung auch aus Gl. (2.150) ableiten.

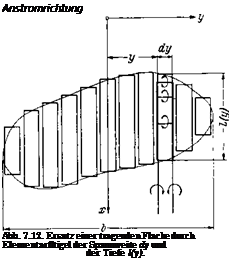Eine zweite Mdglichkeit, den Tragfliigel durch eine Wirbelbelegung darzustellen, besteht darin, daB man nach einem Vorschlag von H. Glauert [18] den Tragfliigel nach Abb. 7.12 durch sogenannte Elemen-

tarfliigel der infinitesimalen Spannweite dy und der Fliigeltiefe l(y) er – setzt. Jedem Elementarfltigel ist im Gesamtverband des Fliigels ein ganz bestimmter, durch die Geometrie des Fliigelgrundrisses gegebener Platz zugeordnet. Das Wirbelsystem jedes Elementarfliigels besteht aus einer Reihe hintereinander Uegender Wirbellinien parallel zur y-Achse und zwei Wirbellinien parallel zur x-Achse, somit aus einer Schar von hinter­einander angeordneten Hufeisenwirbeln, wie sie in Кар. 7.1 eingefiihrt wurden. Diese Darstellung wurde fur einen beliebigen FliigelgrundriB u. a. von E. Truckenbrodt [73] angegeben. In Abb. 7.13 ist fur das Beispiel eines schiebenden Pfeilfltigels das soeben Gesagte noch einmal genauer dargestellt. Zu diesem Bild moge bemerkt werden, daB die freien Wirbel der einzelnen Hufeisenwirbel nur der Deutlichkeit halber nebeneinander

gezeichnet wurden, wahrend sie tatsachlich auf zwei parallelen Linien mit dem Abstand dy liegen. Der Elementarflugel hat in der Richtung der Flxigeltiefe (ж-Richtung) eine Zirkulationsverteilung mit der Dichte

Abb. 7.13. Wirbelsystem eines schiebenden Pfeilflugels nach [75].

k(x) pro Langeneinheit. Fur ein Flachenelement des Elementarfliigels mit der Spannweite dy und der Tiefenerstreckung dx ist die Zirkulation

dT{x, y) — k(x, y) dx. (7.35)

Im Vergleich mit der Darstellung von Abb. 7.11 entspricht к dem dort verwendeten ky. Somit ist nach Gl. (7.33) die Gesamtzirkulation der gebundenen Wirbel des Elementarfliigels

%h(y)

Г(у) = f k(x, y)dx. (7.36)

xvU>)

Die gleiche Zirkulation haben auch die beiden von der Hinterkante des Elementarfliigels abgehenden freien Wirbel.

Im Rahmen der linearen Tragflachentheorie, d. h. bei Beschrankung auf kleine Profilwolbungen der einzelnen Fliigelschnitte und auf kleine Anstellwinkel, kann angenommen werden, daB die gebundenen und die freien Wirbel aller Elementarfliigel in einer Ebene (ж, y-Ebene) liegen. Dieses wurde auch bei der Profiltheorie in Кар. 6.32 vorausgesetzt.