Van der Waals Effects

Thermally perfect gases are gases, for which it can be assumed that its con­stituents have no spatial extension, and no intermolecular forces acting be­tween them, except during actual collisions [1]. This situation is given, if the gas density is small. For such gases the equation of state holds

p = pRT. (5.1)

If at the same time the specific heats at constant pressure cp and constant volume cv are independent of the temperature, we speak about thermally and calorically perfect gases.

If the molecular spacing is comparable to the range of the intermolecu­lar forces, “van der Waals” forces are present. This happens at rather low temperatures and sufficiently high densities/pressures. The equation of state then is written

p = pRTZ (p, T), (5.2)

with Z being the real-gas factor, which is a function of the “virial coefficients” B, C, D, … [2]

Z (p, T) = 1 + pB(T) + p2C (T) + p[42]D(T) + …. (5.3)

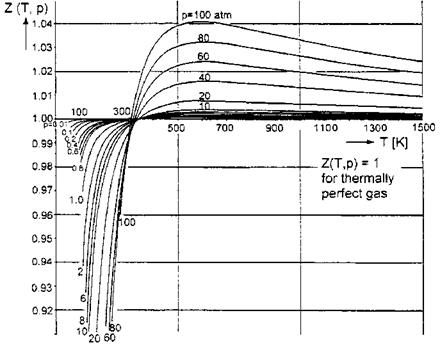
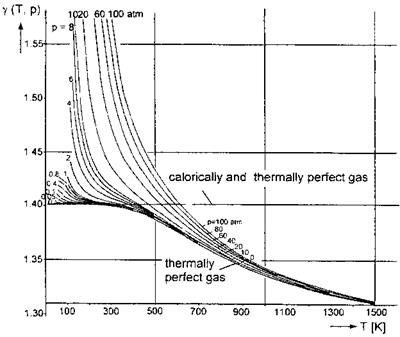
We show for the pressure range: 0 atm < p ^ 100 atm (1 atm = 101,325 Pa), and the temperature range: 0 K < T ^ 1,500 K, the real-gas factor Z(p, T) in Fig. 5.1, and the ratio of specific heats j(p, T) in Fig. 5.2. The data were taken from [3], where they are presented in the cited temperature and pressure range for non-dissociated air with equilibrium vibrational excitation.

Fig. 5.1 exhibits that especially at temperatures below approximately 300 K, and relatively large pressures, and hence densities, van der Waals effects play a role. However, the real-gas factor is rather close to the value one. The same is true for larger temperatures, where even at 10 atm the factor Z is smaller than 1.004.

The ratio of specific heats 7, Fig. 5.2, is similarly insensitive, if the pressure is not too high.3 The critical temperature range, where van der Waals effects appear, even at low pressures, again is below approximately 300 K.

Fig. 5.1. Real-gas factor Z(T, p) of air [3].

In order to get a feeling about the importance of van der Waals effects, we consider the parameter ranges in hypersonic flight, Sections 1.2 and 2.1, and find the qualitative results given in Table 5.1.

Table 5.1. Qualitative consideration of aerothermodynamic parameters in the flight free-stream, and in the stagnation point region of a flight vehicle.

Item	Speed v	Pressure p	Density p	Temperature T	v. d. Waals effects
Free stream	large	small	small	small	small
Stagnation area	small	large	large	large	small

We observe from Table 5.1 that in hypersonic flight obviously the tenden­cies of pressure/density and temperature are against van der Waals effects. In the free stream at small temperatures also pressure/density are small, whereas in the stagnation area at large pressures/density also the tempera­ture is large. Therefore in general we can neglect van der Waals effects in the flight regime covered by hypersonic vehicles in the Earth atmosphere.

Fig. 5.2. Ratio of specific heats y(T, p) of air [3].

The situation can be different with aerothermodynamic ground-simulation facilities with high reservoir pressures at moderate temperatures. Here van der Waals effects can play a role, and hence must be quantified, and, if nec­essary, be taken into account, see, e. g., [4].