Velocity components in terms of ф

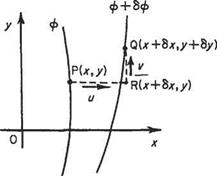
(a) In Cartesian coordinates Let a point P(x, y) be on an equipotential ф and a neighbouring point Q(x + 6x, y + 6y) be on the equipotential ф + 6ф (Fig. 3.4). Then by definition the increase in velocity potential from P to Q is the line integral of the tangential velocity component along any path between P and Q. Taking PRQ as the most convenient path where the local velocity components are и and v:

Fig. 3.4 Thus, equating terms and

(3.2)

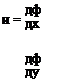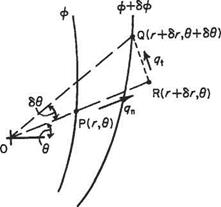
(b) In polar coordinates Let a point P(r, ff) be on an equipotential ф and a neigh­bouring point Q(r + Sr, в + 66) be on an equipotential ф + 6ф (Fig. 3.5). By definition the increase дф is the line integral of the tangential component of velocity along any path. For convenience choose PRQ where point R is (r + 6r, в). Then integrating along PR and RQ where the velocities are qn and qt respectively, and are both in the direction of integration:

бф = qnSr + qt(r + 6r)66

= qn6r + qtr66 to the first order of small quantities.

But, since ф is a function of two independent variables;

сі дф, дф

6ф=Tr6r * дё60

(3.3)

and

1 дф

Again, in general, the velocity q in any direction s is found by differentiating the velocity potential ф partially with respect to the direction s of q:

3.2 Laplace’s equation As a focus of the new ideas met so far that are to be used in this chapter, the main fundamentals are summarized, using Cartesian coordinates for convenience, as follows: (1) The equation of continuity in two dimensions (incompressible flow) du dv

я ‘ + я – — 0 dx ay

(2) The equation of vorticity

dv_dH

(ii)

(3) The stream function (incompressible flow) ip describes a continuous flow in two dimensions where the velocity at any point is given by

dip dx

(iii)

(4) The velocity potential ф describes an irrotational flow in two dimensions where the velocity at any point is given by

дф дф

“ = а~х У = Щ (,v)

Substituting (iii) in (i) gives the identity

d2ip d2ip

dxdy ~ dxdy ~

which demonstrates the validity of (iii), while substituting (iv) in (ii) gives the identity

д2ф д2ф

dxdy dxdy

demonstrating the validity of (iv), i. e. a flow described by a unique velocity potential must be irrotational.

Alternatively substituting (iii) in (ii) and (iv) in (i) the criteria for irrotational continuous flow are that

д2ф д2ф _ д2Ф д2,ф д7- + д?= = ~дх2+Ъу2

also written as Х72ф = Х72ф — 0, where the operator nabla squared

92 d2 dx2 + dy2

Eqn (3.4) is Laplace’s equation.