Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
3D far-field effect of drag
A 3D body with profile drag will have a viscous wake with some velocity defect Auwake(y, z) = u — VL, shown in Figure 2.18. Following the 2D airfoil analysis of Appendix C, the far-field source strength is the integrated volume flow rate of the wake velocity defect, and the profile drag is the associated integrated momentum defect.
£ = — Auwake dy dz (2.108)
Dp = JJ(VL+Auwake)(—Auwake) dy dz (2.109)
The drag derivation will also be given later in Section 5.6.
In the far wake we also have Auwake ^ 0, so that the two relations above can be combined to give the far-held source strength in terms of the profile drag Dp of the body, or equivalently in terms of its profile drag coefficient Cdp based on some reference area Sref.
£ = = lv^SreiCDp (2.110)
 |
pVO 2 p
2.12.1 3D far-field effect of volume
 |
 |
 |
The inviscid flow about a slender body of revolution, such as an airplane fuselage, can be accurately represented by a variable-strength source filament placed along the body centerline, superimposed with a freestream. This model is shown in Figure 2.19.
x
Figure 2.19: Flow about slender body represented by a source filament of variable strength Л(х).
 |
 |
Following the 2D airfoil thickness analysis, the source filament strength Л(х) can be determined by mass conservation applied to the local control volume which has the body’s cross sectional area A(x) and is dx thick in the axial direction. The flow is required to be tangent to the outside perimeter surface of the control volume, so the net outflow from the source filament inside is equal to the volume flow difference between the front and rear faces of area A and A + dA, as given by (2.39). This gives the required source filament strength.
 |
 |
The far-field x-doublet for this source filament is then determined from the KX definition (2.105).
The last integral above can be integrated by parts as in the 2D case, giving a rather simple expression for KX in terms of the body volume V = XTE A dx.
XLE
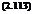Kx = Vo V
 |
 |
 |
The above analysis is strictly valid only if the body is slender, which is a prerequisite for accuracy of the source filament model. For non-slender bodies (2.113) tends to somewhat underpredict the actual far-field doublet strength. For bodies of revolution, an improved empirical estimate is
where dmax is the maximum cross-section diameter and £ = xTE—xLE is the body length. For more general body shapes, dmax can be replaced by л/4Атах/7г, where Amax is the maximum cross-sectional area.
