Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
3D Far-Fields
The 3D potential of a source distribution is given by (2.43), with the kernel’s distance function R again defined for convenience.
<F(r) = 4vr III (T[r’)^ dx’dy’dz’ (2.100)
R = |r —r’| = л/ (x—x1)2 + (y—y1)2 + (z — z’)2 (2.101)
As in the 2D case, the kernel function 1/R is now expanded as a Taylor series about the origin r’ = 0, this time using compact vector notation.
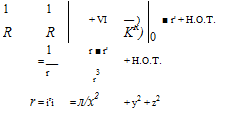(2.102)
 |
 |
 |
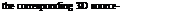
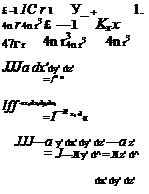Substituting (2.102) into (2.100) and dropping the higher order terms gives far-field approximation.
The second integrals in (2.104)-(2.107) would be used for the case where the starting source distribution is a filament Л(е) rather than a volume source density. Like in the 2D case, a 3D doublet strength K is a vector whose three components depend on the chosen axes. Its being a vector is also what allows (2.103) to have its coordinate-independent form.
