A source set upstream of an equal sink in a uniform stream

The stream function due to this combination is:

Here the first term represents a source and sink combination set with the source to the right of the sink. For the source to be upstream of the sink the uniform stream must be from right to left, i. e. negative. If the source is placed downstream of the sink an entirely different stream pattern is obtained.

The velocity potential at any point in the flow due to this combination is given by:

ф = In — – Ur sin в 2тГ Г2

or

The streamline ф = 0 gives a closed oval curve (not an ellipse), that is symmetrical about the Ox and Оу axes. Flow of stream function ф greater than ф — 0 shows the flow round such an oval set at zero incidence in a uniform stream. Streamlines can be obtained by plotting or by superposition of the separate standard flows (Fig. 3.18). The streamline ф = 0 again separates the flow into two distinct regions. The first is wholly contained within the closed oval and consists of the flow out of the source and into the sink. The second is that of the approaching uniform stream which flows around the oval curve and returns to its uniformity again. Again replacing ф = 0 by a solid boundary, or indeed a solid body whose shape is given by ф = 0, does not influence the flow pattern in any way.

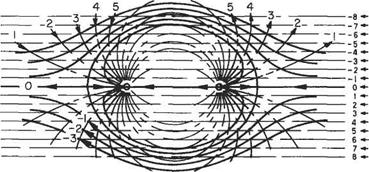Thus the stream function ф of Eqn (3.31) can be used to represent the flow around a long cylinder of oval section set with its major axis parallel to a steady stream. To find the stream function representing a flow round such an oval cylinder it must be possible to obtain m and c (the strengths of the source and sink and distance apart) in terms of the size of the body and the speed of the incident stream.

Suppose there is an oval of breadth 2bo and thickness 2to set in a uniform flow of U. The problem is to find m and c in the stream function, Eqn (3.31), which will then represent the flow round the oval.

(a) The oval must conform to Eqn (3.31):

(b)

On streamline ф = 0 maximum thickness to occurs at x — 0, у = t0. Therefore, substituting in the above equation:

and rearranging

(c) A stagnation point (point where the local velocity is zero) is situated at the ‘nose’ of the oval, i. e. at the point у = 0, x = bo, i. e.:

_ дф d (m _y 2су

дф m 1 (x2 + y2 — c2)2c — 2y 2cy

and putting у = 0 and x — bo with дф/ду = 0:

m {bl – c2)2c _ m 2c _

2тг(г>2_с2)2 2тг bl~c2

Therefore

Л2 – r2

m = irU-Z————————————– (3.35)

c

The simultaneous solution of Eqns (3.34) and (3.35) will furnish values of m and c to satisfy any given set of conditions. Alternatively (a), (b) and (c) above can be used to find the thickness and length of the oval formed by the streamline ф = 0. This form of the problem is more often set in examinations than the preceding one.