Advance per revolution

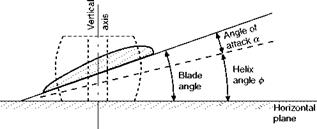
In a propeller, the blade angle at each section is greater than the helix angle and, what is more important, the distance moved forward in one revolution (called the advance per revolution) is not by any means a fixed quantity, as it depends entirely on the forward speed of the aeroplane.

Direction of motion of aeroplane

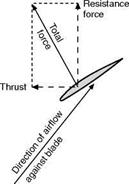
Fig 4.7 Motion of a section of a propeller blade Showing resolution of total force into thrust and resistance

Helical path of A

Helical path of В

Advance

per revolution

Fig 4.8 Helical paths travelled by various sections of propeller blade

Fig 4G Pusher – new type (opposite)

(By courtesy of the Beech Aircraft Corporation, USA)

The Beech Starship. Twin pusher turboprop with many other advanced features including tail-first ‘canard’ configuration.

Fig 4H Pusher and tractor (By courtesy of Cessna Aircraft Company, USA) Unique 4/6 seater with two tandem horizontally opposed air-cooled engines, each driving a 2-blade feathering constant-speed propeller.

Fig 4.10 Blade angle

For instance, if an aeroplane is flying at 100 m/s and the propeller is making 1200 rpm – i. e. 20 revs per second – then the advance per revolution will be 100/20 = 5 metres. But the same aeroplane may fly at 80 m/s, with the same revolutions of the propeller, and the advance per revolution will be only 4 metres; while when the engine is run up on the ground and there is no forward motion, the advance per revolution will obviously be 0.

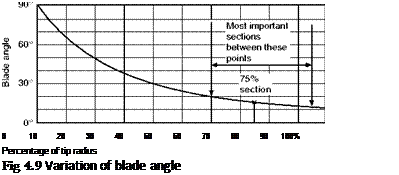
Considering first a fixed-pitch propeller, if the angle of a blade section at a radius of r metres is 0°, and if this particular blade section were to move par­allel to its chord – i. e. so that its angle of attack was 0° – while at the same time it made one complete revolution, then the distance travelled forward, p metres, would be a definite quantity and would correspond to the pitch of an ordinary screw, the relation p = 2кг tan в being true. This is best seen graph­ically by setting off the blade angle в from the distance 2кг drawn horizontally, p being the vertical height. If the same operation is carried out at different dis­tances from the axis of the propeller (Fig. 4.11), it will be found that the value of p is practically the same for all sections of the blade since as the radius r increases there is a corresponding decrease in the blade angle в, and 2кг tan в remains constant.