Aerodynamic Forces and Moments

The aim in performing the real gas flow analysis over bodies is to determine the aerodynamic forces, moments and the heat loads acting. For this purpose the computed pressure and stress fields are integrated over whole surface of the body. The surface stresses are obtained from the velocity gradients calculated at the surface. Let us now write down the x, y and z components of the infinitesimal surface force dF acting on the infinitesimal area dA of the surface

dFx (nxsxx T nysxy T nzsxz)dA

dFy = (uxSyx T nySyy T UzSyZ)dA (2.70)

dFz = (nxszx T uyTzy T uz%Z)dA

Here, ux, uy and uz are the direction cosines of the vector normal to the infin­itesimal surface dA. Let us now express the area dA in curvilinear coordinates. We can express the integral relations which give the total force components in xyz in terms of the differential area given in curvilinear coordinates as shown in

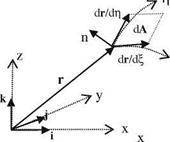
Fig. 2.8.

As seen in Fig. 2.8 the differential area dA can be computed in terms of the product of two infinitesimal vectors given as the changes of the position vector r = xi? yj? zk in directions of П and g coordinates as dA = (dr/d^)x(dr/ dg)|dndg. The vector product of these two vectors also give the direction of the unit normal n of dA. In explicit form we find

= y^Zg – z&g)2+ (x^Zg – z^Xg)2+ {упуп – x^yg)2dn dg (2.71)

Here, the term under the square root is named reduced Jacobian I. The unit normal vector in open form becomes

(ynZg – znygfi – (XnZg – zn xn)j + (ynyg – xnyg)~

We can write the components of the stress tensor in terms of the velocity gradients expressed in curvilinear coordinates as follows for example for sxy

If we consider Equations 2.71-2.73 to form the differential force elements and integrate them numerically over the differential area, we obtain the total force components as follows

Fx = dFx = + + dg

A A

Fy = j dFy = J {uxSyx + nySyy F nzXyz)ldn dg AA

FZ J* dFZ J* {nxszx F nyszy F nzszz)1dn dg

AA

Computations of the moments with respect to a point can be performed simi­larly with considering the moment arm of the point to the differential area dA.

In case of two dimensional incompressible external flows if we know the

d

vorticity field x, first the surface vortex sheet strength у = J x dy is determined.

0

Afterwards, we can compute the aerodynamic force acting on an airfoil as follows (Wu)

d d

q rx( у — Fxns)dBs — q rxFdR (2-75)

B

Here, ns is the unit normal to the airfoil surface and Vxns is the velocity tangent to the surface. For a pitching and plunging airfoil, the value of the tangential velocity is computed at every discrete point on the surface and used in Eq. 2.75.