Autorotational Performance

The autorotation maneuver has been discussed in Section 2.13.7 and is defined as a self-sustained rotation of the rotor without the application of any shaft torque from the engine (i. e., Cq ~ 0). Under these conditions, the power to drive the rotor comes from the relative airstream upward through the rotor as the helicopter descends through the air.

Autorotation is used as a means of recovering the safe flight helicopter in the event of a catastrophic mechanical failure, such as engine, transmission, or tail rotor failure. The ability to autorotate is, therefore, a safety of flight issue. Under established autorotative conditions, there is an energy balance where the decrease in aircraft potential energy per unit time is equal to the power required to sustain the rotor speed. In other words, the pilot gives up altitude at a controlled rate in return for energy to turn the rotor to keep it producing thrust. Recall from Section 2.13.7 that an autorotation at low forward flight speeds will take place in the turbulent wake state where the flow is not smooth and leads to a certain amount of unsteadiness at. the rotor. At higher forward speeds the flow through the rotor tends to be smoother in the autorotational condition.

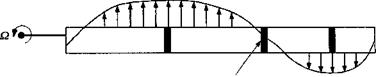
Consider now the flow environment encountered at a blade element on the rotor during a descent, as shown in Fig. 5.24. Although most autorotations are conducted with some forward speed, first consider a vertical autorotative descent with no forward speed. In an autorotation, the inflow angle ф must be such that there is no net in-plane force and, therefore, no contribution to rotor torque, that is, for this station on the blade,

dQ = (D – фЬ)у dy = 0. (5.82)

However, this is a condition that can only exist at most at two radial stations on the blade. In general, some stations on the rotor will absorb power from the relative airstream and some will consume power such that the net power at the rotor shaft is approximately zero. With

/2-

Section ІП/ autorotational At section ул equilibrium

net positive in-plane force (delivers power to rotor)

Driving force
*] Thrust force

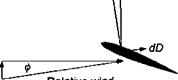Relative wind

NOTE: Angles exaggerated for clarity

the assumption of uniform inflow over the disk, the induced AoA is given by

It follows that the induced angles of attack over the inboard stations of the blade are high, and near the tip ф is low. Therefore, we find that at the inboard part of the blade the net AoA results in a forward inclination of the sectional lift vector and is such that in this region there is now a negative induced drag component that is greater than the profile drag. Therefore, this blade element absorbs power from the airstream to the rotor. At the tip of the blade where ф is low, these sections consume power because, as a result of the forward inclination of the lift vector, the propulsive component is insufficient to overcome the profile drag. The effect is summarized in Fig. 5.24. The consequences are that after initial autorotational equilibrium is obtained, variations in rotor thrust, inflow, and so on, will cause rotor rpm (£2) to adjust itself automatically until autorotational equilibrium is again obtained. Generally, autorotation is a stable equilibrium point because if Q increases, ф will decrease and the region of accelerating torque will decrease inboard, and this tends to decrease rotor rpm. Conversely, if the rotor rpm decreases then ф will increase and the region of accelerating torque will grow outward.

Consider the autorotation diagram shown in Fig. 5.25, where the blade section Cd/Ci is plotted versus AoA at the blade section. This is a form originally used by Wimperis (1928). Both Nikolsky (1944) and Gessow & Myers (1952) describe rotor equilibrium at the blade element in terms of this interpretation, which is relatively useful for a further understanding

Figure 5.25 Autorotative diagram used to describe equilibrium conditions at the blade element. Adapted from Gessow & Myers (1952).

of the phenomenon. For a single section in equilibrium recall that

where 6 is the blade pitch angle. For a given value of blade pitch angle, в, and inflow angle ф, the previous equation represents a series of points that form a straight line, which is plotted on Fig. 5.25. The intersection of this line with the measured Q/Q data at point A corresponds to the equilibrium condition where ф — Cd/Ci. Above this point, say at point В, ф > Cd fCr, so this represents an accelerating torque condition. Point C is where Ф < Cd/Сг, this represents a decelerating torque condition. Note that above a certain pitch angle, say 0max, equilibrium is not possible and so for operation at point D stall will occur causing the rotor rpm to decay.

Establishing stable autorotational flight requires a certain level of skill from the pilot. The rotor rpm and the rate of descent can be controlled by the pilot by means of judicious adjustment of the collective pitch setting. The cyclic pitch is used to control the airspeed. The collective controls the mean blade pitch (and hence the mean aerodynamic angles of attack at the blade sections) and, therefore, the blade mean lift, drag, and rotor rpm. In an autorotation the collective pitch is always held at a low value. The inboard parts of the rotor blades always operate at high angles of attack during the autorotative descent. Therefore, the pilot must ensure that the collective pitch angle is kept low enough to prevent stall propagating out from the blade root region, which will tend to quickly decrease rotor rpm because of the high profile drag associated with stall.

The initial stages of the autorotative maneuver are the most critical. During these initial stages, the pilot must sharply lower the collective pitch setting from the normal flight value to prevent blade stall and a rapid decay in rotor rpm. Both military and civil certification requirements impose a finite time delay (usually a few seconds) to account for normal pilot reaction time before the collective pitch is lowered; thus there is always some safety margin imposed in all helicopter designs – see Prouty (1986). However, in most cases the pilot must still react sufficiently quickly to ensure that the rotor rpm does not decay below acceptable margins, this usually being only a matter of seconds.

How quickly the rotor rpm decays is a function of the power required at the time of failure and the rotational kinetic energy of the rotor. Stewart & Sissingh (1949), Newman (1994), and Johnson (1980) give a good summary of this problem, although an approximate but accurate analysis is given by McCormick (1956). The equation of motion for the decay of the rotor rotational speed with time t after the removal for the shaft torque at time t = 0 is

where Ir is the net inertia of the rotor system and the subscript 0 refers to time t = 0. This assumes that the helicopter does not reach an appreciable rate of descent or that the collective pitch is changed. The minus sign on the right-hand side of the foregoing equation denotes a decelerating torque. Integrating Eq. 5.85 by means of separation of variables gives

and the corresponding buildup in rate of descent is

The time constant т is

Notice that KEq is simply the rotational kinetic energy of the rotor at t = 0. This means that rotors with higher initial levels of stored kinetic energy and lower power requirements (i. e., rotors with the lowest disk loading) will have the slowest rate of rpm decay after the removal of shaft torque and the slowest initial rate of descent. See also Section 5.6.3.

Generally, values of r are found to vary from as low as about 1.5 seconds for the biggest and heaviest helicopters to about 4 seconds for the smallest and lightest helicopters. This means that for a typical helicopter the time for the rotor rpm to decay significantly is at most only a few’ seconds, and so the pilot’s reaction to engine or transmission failure must be almost immediate. In the first instance, this will require a rapid reduction of collective pitch. In the second instance, the pilot will generally use cyclic pitch to seek the forward flight airspeed that will give the lowest autorotational rate of descent.

The safe rpm range in autorotation for most helicopters is usually between 80 and 120% of the normal rotor rpm, which is controlled by the pilot primarily by using collective pitch. If the rpm becomes too low, the rotor will begin to stall and excessive blade flapping will also occur because of reduced centrifugal effects on the blades. Conversely, if the rotor rpm becomes too high, then structural overload becomes a concern.