Axisymmetric flow from a point source (or towards a point sink)

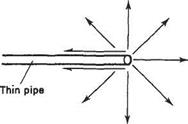
The point source and sink are similar in concept to the line source and sink discussed in Section 3.3. A close physical analogy can be found if one imagines the flow into or out of a very (strictly infinitely) thin round pipe – as depicted in Fig. 3.29. As suggested in this figure the streamlines would be purely radial in direction.

Let us suppose that the flow rate out of the point source is given by Q. Q is usually referred to as the strength of the point source. Now since the flow is purely radial away from the source the total flow rate across the surface of any sphere having its centre at the source will also be Q. (Note that this sphere is purely notional and does not represent a solid body or in any way hinder the flow.) Thus the radial velocity component at any radius R is related to Q as follows

4ttR2qR – Q

It therefore follows from Eqn (3.60) that

_дф _ Q 4R dR 4ttR2

Integration then gives the expression for the velocity potential of a point source as

, Q

4vr R

In a similar fashion an expression for stream function can be derived using Eqn (3.62) giving

ф = — — cos p
4-7Г