Basic Data Processing

The most basic processing procedure in the intensity-based method for PSP and TSP is taking a ratio between the wind-on image and the wind-off reference image to correct the effects of non-homogenous illumination, uneven paint thickness and non-uniform luminophore concentration. However, this ratioing procedure is complicated by model deformation induced by aerodynamic loads, which results in misalignment between the wind-on and wind-off images. Therefore, additional correction procedures are required to eliminate (or reduce) the error sources associated with model deformation, the temperature effect of PSP, self­illumination, and camera noises (dark current and fixed pattern noise).

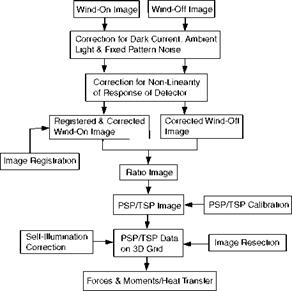
Figure 4.6 shows a generic data processing flowchart for intensity-based measurements of PSP and TSP with a CCD camera. A laser scanning system has similar data processing procedures for intensity-based measurements. The wind – on and wind-off images are acquired using a CCD camera. Usually, a sequence of acquired images is averaged to reduce the random noise like the photon shot noise. The dark current image and ambient lighting image are subtracted from data images to eliminate the dark current noise of the CCD camera and the contribution from the ambient light. The dark current image is usually acquired when the camera shutter is closed. In a wind tunnel environment, there is always weak ambient light that may cause a bias error in data images. The ambient lighting image is acquired when the shutter is open while all controllable light sources are turned off. The integration time for the dark current image and ambient lighting image should be the same as that for data images. The data images are then divided by the flat-field image to correct the fixed pattern noise. At a very high signal level, this correction is necessary since the fixed pattern noise may surpass the photon shot noise. Ideally, the flat-field image is acquired from a uniformly illuminated scene. A simple but less accurate approach is use of several diffuse scattering glasses mounted in the front of the lens of the camera to generate an approximately uniform illumination field. When a uniform illumination field cannot be achieved, a more complex noise-model-based approach can be used to obtain the fixed pattern noise field for a CCD camera (Healey and Kondepudy 1994). Normally, a scientific grade CCD camera has a good linear response of the camera output to the incident irradiance of light. However, conventional CCD video cameras often exhibit a non-linear response to the incident light intensity; in this case, a video camera should be radiometrically calibrated to correct the non-linearity. A simple but useful radiometric camera calibration technique is described in Chapter 5.

In this stage, even though the noise-corrected wind-on and wind-off images are obtained, we cannot yet calculate a ratio of the wind-off image over the wind-on image, Vref/V, for conversion to a pressure or temperature image. This is

because the wind-on image may not align with the wind-off image due to model deformation produced by aerodynamic loads. A ratio between those non-aligned images can lead to a considerable error in calculation of pressure or temperature using a calibration relation. Also, some distinct flow features such as shock, boundary layer transition and flow separation could be smeared. In order to correct the non-alignment problem, the image registration technique should be used to match the wind-on image to the wind-off image (Bell and McLachlan 1993, 1996; Donovan et al. 1993). The image registration technique is based on a mathematical transformation (x’,y’) ^ (x, y), which empirically maps the deformed wind-on image coordinate (X, y’) onto the reference wind-off image coordinate (x, y). For a small deformation, an image registration transformation is well described by polynomials

m m

(x, y) = (^ aijXiy’i, ^). (4.28)

i, j =0 i, j =0

Geometrically, the constant terms, linear terms, non-linear terms in Eq. (4.28) represent translation, rotation and scaling, and higher-order deformation of a model in the image plane, respectively. In measurements of PSP and TSP, black fiducial targets are placed in the locations on a model where deformation is appreciable. The displacement of these marks in the image plane represents perspective projection of real model deformation in the 3D object space. From the corresponding centroids of the targets in the wind-on and wind-off images, the polynomial coefficients a{j and by in Eq. (4.28) can be determined using

least-squares method. More targets will increase the statistical redundancy and improve the precision of least-squares estimation. For most wind tunnel tests, a second-order polynomial transformation (m = 2) is found to be sufficient. As a pure geometric correction method, however, the image registration technique fails to take into account a variation in illumination level on a model due to model movement in a non-homogenous illumination field. An estimate of this error requires the knowledge of the illumination field and the movement of the model relative to the light sources. Bell and McLachlan (1993, 1996) gave an analysis on this error in a simplified circumstance and found that this error was small if the illumination light field was nearly homogenous and model movement was small. Experiments showed that the image registration

technique considerably improved the quality of PSP and TSP images (McLachlan and Bell 1995). Weaver et al. (1999) utilized spatial anomalies (dots formed from aerosol mists in spraying) in a basecoat and calculated a pixel shift vector field of a model using a spatial correlation technique similar to that used in particle image velocimetry (PIV). Based on the shift vector field, the wind-on image was registered. Le Sant et al. (1997) described an automatic scheme for target recognition and image alignment. A detailed discussion on the image registration technique is given in Chapter 5.

After a ratio of the wind-off image over the registered wind-on image is taken, a pressure or temperature image can be obtained using the calibration relation (the Stern-Volmer relation for PSP or the Arrhenius relation for TSP). Compared to relatively straightforward conversion of an intensity ratio image to a temperature image, conversion to a pressure image is more difficult since the intensity ratio image of PSP is a function of not only pressure, but also temperature. The temperature effect of PSP often has a dominant contribution to the total uncertainty of PSP measurements if it is not corrected. When the Stern-Volmer coefficients A(T) and B(T) are determined in a priori laboratory PSP calibration and the temperature field on the surface are known, the pressure field can be, in principle, calculated from a ratio image. The need of temperature correction provoked the development of multiple-luminophore PSP and tandem use of PSP with TSP. The surface temperature distribution can be measured using TSP and infrared (IR) cameras. Also, the temperature field can be given by theoretical and numerical solutions to the motion and energy equations of flows. Unfortunately, experiments have shown that the use of a priori laboratory PSP calibration with a correction for the temperature effect still leads to a systematic error in the derived pressure distribution due to certain uncontrollable factors in wind tunnel environment. To correct this systematic error, pressure tap data at a number of locations are used to correlate the intensity ratio values to the pressure tap data; this procedure is referred to as in-situ calibration of PSP. In the worst case where A(T) and B(T) are not known and the surface temperature field is not given, in-situ calibration is still able to give a pressure field. However, the accuracy of interpretation of PSP data between the pressure taps is not guaranteed especially when the gradients of the pressure and temperature fields between the taps are large. Obviously, the selection of the locations of the pressure taps is critical to assure the accuracy of in-situ calibration. The pressure tap data at the discrete locations for in-situ calibration should reasonably cover the pressure distribution on the surface. The in-situ calibration uncertainty of PSP is discussed in Chapter 7.

PSP and TSP data in images have to be mapped onto a surface grid of a model in the 3D object space since the pressure and temperature fields on the surface grid are more useful for engineers and researchers. Further, this mapping is necessary for extraction of aerodynamic loads and heat transfer and for comparison with CFD results. In the literature of PSP and TSP, this mapping procedure is often called image resection. Note that the meaning of resection in the PSP and TSP literature is somewhat broader and looser than the strict one in photogrammetry. From the standpoint of photogrammetry, a key of this procedure is geometric camera calibration by solving the perspective collinearity equations to determine the camera interior and exterior orientation parameters, and lens distortion parameters. Once these parameters in the collinearity equations relating the 3D object space to the image plane are known, PSP and TSP data in images can be mapped onto a given surface grid in the 3D object space. A detailed discussion on analytical photogrammetric techniques is given in Chapter 5. In most PSP and TSP measurements conducted so far, data in images are mapped onto a rigid CFD or CAD surface grid of a model. However, when a model experiences a significant aeroelastic deformation in wind tunnel tests, mapping onto a rigid grid misrepresents the true pressure and temperature fields. Therefore, a deformed surface grid of a model should be generated for PSP and TSP mapping. Liu et al. (1999) discussed generation of a deformed surface grid based on videogrammetric model deformation measurements conducted along with PSP/TSP measurements (see Chapter 5). Finally, the integrated aerodynamic forces and moments can be calculated from the pressure distribution on the surface. For example, the lift is given by FL = ^ pt(n • lLAS ), where n is the unit normal vector of a panel on the surface, AS is the area of the panel, and lL is the unit vector of the lift. Similarly, the integrated quantities of heat transfer can be obtained from the surface temperature fields based on appropriate heat transfer models.

The self-illumination correction is implemented after the luminescent intensity data are mapped on a surface grid in the 3D object space. The so – called self-illumination is a phenomenon that the luminescent emission from one part of a model surface illuminates another surface, thus increasing the observed luminescent intensity of the receiving surface and producing an additional error in calculation of pressure and temperature. This distorting effect often occurs on the surfaces of neighboring components such as wind/body junctures and concave surfaces. The self-illumination depends on the surface geometry, the luminescent field, and the reflecting properties of a paint layer. Assuming that a paint surface is Lambertian, Ruyten (1997a, 1997b, 2001a) developed an analytical model and a numerical scheme for correcting the self-illumination effect. The self-illumination correction scheme is discussed in Chapter 5.

One of the original purposes of developing two-luminophore PSPs is to simplify the data processing for PSP. The dependency of a two-color intensity ratio ІЯі /1 Яі on pressure p and temperature T is generally expressed as

І я /112 = f(p, T), where 1 я and 1^ are the luminescent intensities at the emission wavelengths Я1 and Я2, respectively. Ideally, a two-color intensity ratio can eliminate the effect of spatially non-uniform illumination on a surface. However, since two luminophores cannot be perfectly mixed, the simple two – color intensity ratio Ія /1^ cannot completely compensate the effect of non­homogenous dye concentration. In this case, a ratio of ratios (І я / І я )/(І я / І я )0 should be used to correct the effects of non-homogenous

dye concentration and paint thickness variation, where the subscript 0 denotes the wind-off condition (McLean 1998). Since the wind-off images are required, the ratio-of-ratios method still needs image registration. The ratio-of-ratios approach was also applied to non-pressure-sensitive reference targets to compensate the effect of non-homogenous illumination on a moving model (Subramanian et al. 2002).