Compressible 3D finite wing

Consider a simple, flat rectangular wing with aspect ratio AR and an uncambered airfoil. The objective is to determine its Cl and CD for a given angle of attack a and freestream Mach. Following the PG solution procedure we transform this to x, y,C space where the corresponding transformed wing has

AR = в AR (8.83)

a = в a (8.84)

and its flow-field is governed by the Laplace equation for ф. For a high aspect ratio wing this is approx­imately solved by classical lifting line theory given in Appendix E. The final results for the lift coeffi­cient (E.37) and induced drag coefficient (E.23) can then be directly applied to the transformed problem,

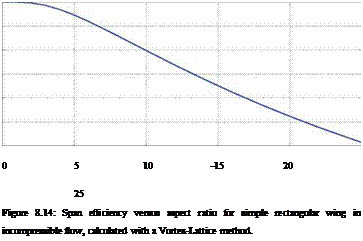
where cfa ~ 2n is the wing airfoil’s 2D lift-curve slope. An offset to a from the wing airfoil camber has been omitted from (8.85), so that a is in effect measured from the transformed wing airfoil’s zero-lift line. The span efficiency e(2R) depends on the transformed wing’s aspect ratio, as shown in Figure 8.14.

1

0.98 0.96

e

0.94 0.92 0.9 0.88

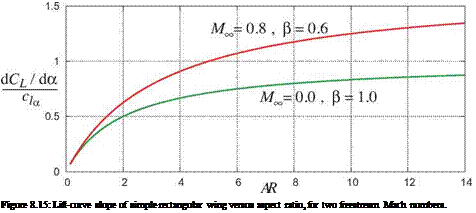The 3D lift-curve slope of the wing dCL/да is now seen to depend on в as well as AR, as plotted in Figure 8.18. Two limiting cases or interest are

For a given Cl, the C^ is seen to be mostly unaffected by compressibility, except via the small effect of the span efficiency e which decreases slightly with AR. For a near-elliptical planform we would have e ~ 1,
in which case CD would be essentially independent of ML. This insensitivity of CD to the aircraft flight Mach is consistent with Trefftz-plane theory, in which the lift and the induced drag are implicitly related to each other via the aircraft’s trailing vorticity distribution. The aircraft’s compressible near-field has no bearing on this lift and induced drag relation.