DRA2303 Transonic Profile

The DRA2303 transonic airfoil [10] was chosen as the aerodynamic reference case for the buffet phenomenon. Associated with buffet are self-sustained shock wave oscillations on airfoils at transonic flow. The flow configuration, which was to lie well within the buffet boundaries, was chosen with Ma = 0.72, Re = 2.6 • 106 and a = 3°. For this flow configuration, experimental data is not yet available.

In this work the buffet is computationally targeted with three different simu­lations: a full domain RANS-simulation based on the Baldwin-Lomax turbulence model [1], a full domain LES which constitutes the reference solution and a fully coupled zonal RANS-LES solution. First, the full LES solution of the DRA2303 is investigated. The RANS simulation, which was also a calibration case for the sensor in section 3.1, is compared with the reference LES solution. Finally, a fully coupled zonal RANS-LES solution yielding preliminary results is presented. The numerical details of the full LES solution and the zonal RANS-LES are given in Tab. 7 and Tab. 8, respectively. Similar to the SWBLI case the number of required grid points

	streamwise x	wall normal y	spanwise z
Domain size in c	20	20	0.021
Grid points (30.4-106	2364	130	99
Resolution, wall units	Ax+ – 100	Ay+ 1.0 min	Az+ – 20

for the zonal RANS-LES simulation contains less than 50 % of the grid points used in the full domain LES simulation.

The focus of this numerical investigation using a full RANS simulation was on the evaluation of the reduced frequency a* = ac/U^ for the given flow configura­tion. In Fig. 13 the instantaneous pressure coefficients cp and the average pressure coefficient fluctuation at the upper side of the airfoil for the full RANS simulation are shown. At this flow configuration the extension of the horizontal shock move­ment is about 0.25 c. High level pressure fluctuations are found downstream of the shock, especially near the trailing edge where the strength of these fluctuations even exceeds the pressure amplitude of the shock.

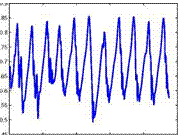Fig. 13 Fluctuating wall pressure coefficient Cp (left) and corresponding rms-values at the upper side of the profile (right) for a RANS simulation

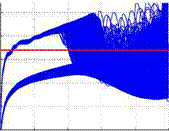
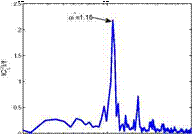
Fig. 14 Fourier transformed fluctuations of the lift coefficient Cl and corresponding fluctu­ations over time for a RANS simulation

In Fig. 14 the lift coefficient is investigated. The shock oscillation is highly peri­odic indicated by the pronounced peak in Fig. 14 (left). The reduced frequency shows a value of 1.16 which is about twice as high as it was expected from exper­iments at higher Reynolds numbers [28] and it is known that the influence of the Reynolds number on the reduced frequency is small [17]. The amplitude of the lift coefficient ACl is about 0.3 (see Fig. 14, right). It is known from previous numer­ical investigations [26] that for the DRA2303 case the reduced frequencies of the RANS simulations were far off the expected values. However, numerical investiga­tions with RANS on other airfoil types proved to be much more promising and more successful than for the DRA2303 case [22].

For this reason, a full LES simulation was set up to examine the physical aspects of buffet without using standard turbulence models. The simulation time for this configuration was about 40c/Ц» which can be considered as a long term simulation where effects of initial perturbations or flow developing effects possess no influence anymore on the solution and a periodic flow behavior determines the result.

In Fig. 15 the instantaneous pressure coefficient cp and the average pressure coef­ficient fluctuations at the upper side of the profile are presented. Note that the ex­tension of the horizontal shock oscillation is about 0.07 c. That is much smaller compared to the outcome of the RANS simulation. The peak in the average pressure fluctuations is more pronounced (compare Fig. 13, right) and near the trailing edge the intensity of the fluctuations increases but they never exceed the strength of the shock. Upstream of the shock the pressure fluctuations are very small compared to the fluctuations at the shock position and downstream of the shock. The reduced frequency a* of the lift coefficient oscillation of the full LES solution presented in Fig. 16 is about 0.74 and thus much lower than the one obtained by the RANS simulation. Again, the oscillation is highly periodic which is indicated by the peak in the frequency spectrum. The amplitude of the lift coefficient ACl « 0.03 is small compared to that of the RANS simulation. This finding is due to the smaller ho­rizontal shock oscillation amplitude and the less pronounced pressure fluctuations downstream of the shock.

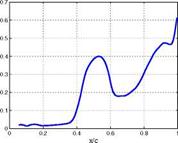
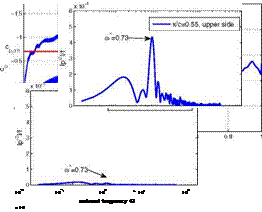
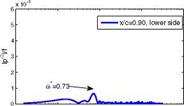
Figure 17 compares the fluctuating pressure intensity at different locations. At the upper side at 0.25 c the amplitude of the fluctuation is very low, however, a small distinctive bump is evident at a* « 0.7. Near the shock at 0.55 c a peak oc­curs at the reduced frequency a* = 0.74 and the distribution of the values is very similar to that in Fig. 16. Close to the trailing edge at 0.9 c the major peak is still at a* « 0.73 but the pressure fluctuations at higher reduced frequencies have grown stronger compared to the position near the shock. This is due to the turbulent shear layer which is at this flow configuration maximum in size at the trailing edge. Al­though the pressure fluctuations are averaged in the spanwise direction the pressure fluctuations at very high reduced frequencies can be related to the turbulent shear layer. At the lower side of the profile at 0.9 c the intensity level of the fluctuations is one order of magnitude smaller compared with the corresponding position at the upper side. However, a distinct peak at a* « 0.73 is visible which is caused by the direct influence of the oscillating shock at the upper side.

Fig. 15 Fluctuating wall pressure coefficient Cp (left) and corresponding rms-values at the upper side of the profile (right) for an LES simulation

X 10 [2]

– x/c=0.90, upper side I

© =0.73

….

Fig. 17 Fourier transformed pressure fluctuations at different positions of the DRA2303 airfoil

Fig. 18 Reynolds shear stresses at two different positions at the DRA2303-profile: at x/c = 0.4 (left) and x/c = 0.6

The Reynolds shear stresses of the averaged full LES solution at two different locations is exhibited in Fig. 18. At 0.4 c the distribution resembles that of a flat plate boundary layer flow and its turbulent features. Behind the shock, however, the maxima of all components moves to the center of the boundary layer and the intensity level of (v’v’), (w’w’), and (u! v’) is much higher compared with the pos­ition ahead of the shock. Downstream of the shock the intensities of (u’u’), (v’v’), and (Ww’) are at the same level which indicates that the turbulent structures show an isotropic behavior compared with the high level of anisotropy of the near-wall turbulence upstream of the shock.

The A2-contours [13] are shown in Fig. 19. After the interaction with the shock, the turbulent boundary layer separates and a shear flow is formed that develops large coherent structures that convect near the trailing edge. These large structures are responsible for the high level pressure oscillations at high frequencies near the trailing edge.

Due to the very different transient behavior regarding buffet and the subsequent consequences for the boundary layer downstream of the shock location the rms

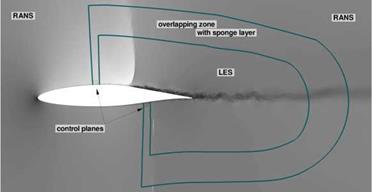
Fig. 20 Computational setup of a fully coupled zonal RANS-LES simulation

values of the pressure coefficient fluctuations diverge in the region between 0.4 c and the trailing edge at the upper side of the airfoil (figs. 13 and 15). Because of the known drawbacks of RANS simulations (see section 1) a zonal RANS-LES compu­tation was set up to overcome the turbulence modeling issue at the shock location and downstream of it. The extent of the LES domain was chosen like in the evalu­ation of the sensor results which have been discussed in section 3.1. The resulting computational set up is shown in Fig. 20. Due to the complexity of this particular case the results can be considered just preliminary.

At the inlet of the LES domain on the upper and lower side of the airfoil, the zonal SEM approach (see section 2.3) is used to generate synthetic turbulent structures. Downstream of the inlet four control planes are located between 0.37 c and 0.4 c at the upper side and between 0.7 c and 0.73 c.

Since pressure waves, caused by the transient shock behavior, travel from the LES domain to the RANS domain and vice versa the time window where the solutions are averaged has to be carefully defined. On the one hand, the turbulent flow properties of the LES solution have to be averaged properly over a sufficiently large time window before being transferred to the RANS domain. On the other hand, the amplitude and frequency of the traveling pressure waves caused by the shock must be captured in a time window which is as small as possible to prevent a signi­ficant alteration of the pressure wave signal. A time window of the size of 1 c/U^ was found to satisfy these requirements.

Table 8 Numerical details of the LES domain for the zonal RANS-LES simulation streamwise x wall normal y spanwise г Grid points (13.7-106) Resolution, wall units 1430 4x+ « 35 97 99 4z+ « 20

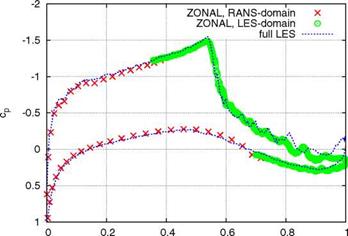
x/c Fig. 21 Comparison of instantaneous wall pressure coefficient Cp between full domain LES and zonal RANS-LES computation

Fig. 22 Я2 structures of transonic flow around a DRA2303 airfoil for a fully coupled zonal RANS-LES solution

In Fig. 21 the instantaneous pressure coefficients cp are given. The zonal RANS – LES solution shows a good agreement with the full LES solution concerning shock position and strength. Downstream of the shock the cp evolution shows minor dis­crepancies near the trailing edge. However, upstream of the shock the zonal RANS – LES results agree pretty well with the findings of the full LES. Note the smooth transition from RANS to LES of the pressure coefficient near the overlapping zones at approximately 0.37 c (upper side) and 0.7 c (lower side).

The A2-contours of the instantaneous zonal RANS-LES solution are depicted in Fig. 22. They show the same features compared to the contours of the full LES simulation such as large coherent structures downstream of the shock interaction zone convecting towards the trailing edge.

4 Conclusion

In this article, a sensor was presented which is capable of detecting flow regions of RANS simulations, where the intricacy of the flow field requires a higher or­der turbulence model. This sensor was applied to several flow cases with complex flow phenomena such as transonic airfoil flow with buffet, or shock wave turbu­lent boundary-layer interaction. For these specific cases the flow regions, where the structure of the flow is highly complex, were replaced by LES domains. To couple the RANS with the LES domain synthetic turbulence generating approaches and control planes were used which transferred the turbulent intensities of the RANS solution to the LES domain. Two different STGM were tested and validated for a subsonic zero pressure gradient boundary layer flow (see section 3). The zonal SEM approach was found to be superior compared to the zonal Batten approach and therefore used in subsequent computations.

Different configurations of control planes were tested on a supersonic zero pres­sure gradient boundary layer flow to evaluate the quality of the transition from the introduced synthetic turbulent structures to fully turbulent flow.

The case where an oblique shock impinges on a compressible turbulent boundary layer was numerically investigated and discussed. First, the sensor detected the re­quired size of the required LES domain by evaluating the corresponding full domain RANS solution. Second, the RANS domain was coupled with the LES region by the zonal SEM approach and control planes downstream of the inlet. This constituted the transition from RANS to LES. The transition from the LES back to the RANS domain was done by applying the approach of Konig et al. [15]. The results have shown that the full domain LES and the zonal RANS-LES provided superior solu­tions compared to a full domain RANS simulation. The extension of the required LES domain in the zonal RANS-LES approach was well predicted by the sensor.

Finally, the computational results of the DRA2303 airfoil in a transonic flow con­figuration were thoroughly discussed. The results of a full domain RANS and full domain LES were compared and the sensor was applied to the RANS solution. The resulting LES domain extensions were implemented into a zonal grid. The coupled zonal RANS-LES approach provided preliminary results and indicates that the qual­ity of the solution is comparable to that of the full domain LES solution.

These two presented cases have shown that the solution computed by a zonal RANS-LES simulation agree well with the corresponding full domain LES solu­tions. However, the computational costs due to the considerable reduction of grid points were reduced by a factor of 2.