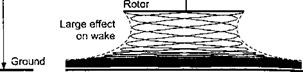
Ground Effect

Helicopter performance is affected by the presence of the ground or any other boundary that may alter or constrain the flow into the rotor or constrain the development of the rotor wake. The effect has long been recognized, but the aerodynamics of the rotor under these conditions are still not fully understood. “Ground effect” is of concern both in actual flight operations as well as in the wind tunnel or hover tower testing of rotors.

(b) In ground effect (IGE)

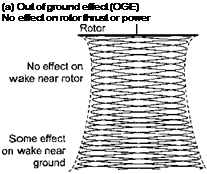
Large effect on rotor thrust and/or power

Rotor height n off the ground

5.8.1 Hovering Flight Near the Ground

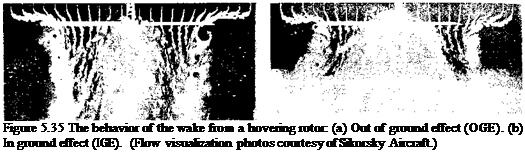
Consider a rotor hovering in close proximity to the ground, as shown in Fig. 5.35. Because the ground must be a streamline to the flow, the rotor slipstream tends to rapidly expand as it approaches the surface. This alters the slipstream velocity, the induced velocity in the plane of the rotor, and, therefore, the rotor thrust and power. Similar effects are obtained both in hover and forward flight, but the effects are strongest in the hovering state. Other visualization of the flow of hovering rotors operating in ground effect are shown by Taylor (1950) and Light & Norman (1989). Systematic studies of rotors operating in ground effect were first conducted by Knight & Hefner (1941).

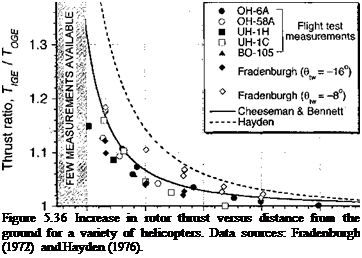
When the hovering rotor is operating in ground effect, the rotor thrust is found to be increased for a given power. A representative plot of the thrust ratio in hover versus height from the ground is shown in Fig. 5.36. This plot has been derived from several experiments with rotors operating at different blade loadings, as discussed by Zbrozek (1947) and others, including Betz (1937), Knight & Hefner (1941), Cheeseman & Bennett (1955), Fradenburgh (1960,1972), Stepniewski & Keys (1984), and Prouty (1985). Hayden (1976) gives a com­prehensive summary of flight test measurements of ground effect using the standardized technique of Lewis (1972). The results suggest significant effects on hovering performance for heights less than one rotor diameter. The results are also dependent somewhat on blade loading (or mean lift coefficient), blade aspect ratio, and blade twist. Yet, within the bounds dictated by most helicopters a universal behavior seems a good approximation for engi­neering estimates of the phenomenon. Besides the effects on actual helicopter performance, these results provide useful guidelines for laboratory testing of rotors in hovering flight,

0.5 1 1.5 2 2.5 3

helicopters. Data sources: Fradenburgh (1972) and Hayden (1976). ” width=”362″ height=”258″/>

Height above ground, z / R

where a minimum distance of at least 2R from the ground is required to ensure performance measurements that are free of interference effects.

The problem of ground effect can also be viewed as a reduction in power for a given thrust. Most of the power reduction is induced in nature, but there is also some small re­duction in profile power because the blade angles are operating at a somewhat lower AoA to produce the same thrust. Because of ground effect there is an important operational advantage to be gained, namely that the lower power required will allow the helicopter to hover in ground effect (IGE) at a higher gross weight or density altitude than would be possible out of ground effect (OGE). The extra thrust or reduction in power require­ments that is felt near the ground will also “cushion” the descent of the helicopter when landing.

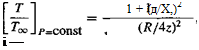Ground effect in hovering flight has been examined analytically, albeit approximately, by means of the method of images. Cheeseman & Bennett (1955) replaced the rotor by a simple source with an image source to simulate ground effect and obtained some analytic relationships for the effects of the ground. Knight & Hefner (1941) and Rossow (1985) have used a vortex cylinder model. Based on Cheeseman & Bennett’s analysis, ground effect on the rotor thrust can be expressed by the equation

where z is the height off the ground and X,- is the induced velocity at the rotor. This equation has a validity of z/R > 0.5. Incorporating the effect of blade loading they obtained

(5.97)

although Ст /о – has a secondary effect. For hovering flight and neglecting any blade-loading effects this latter result simply becomes

=——— l—— -. (5.98)

[°ojp=const 1 — (Я/4 z)

Figure 5.36 shows that this equation gives good agreement with the experimental mea­surements. Because ground effect can be expressed in terms of the increase in thrust at a constant power, then Хюе Ctige — Xoge Ctoge or

X/ge _ Tqge

xOGE TlGE

Alternatively, the influence of ground effect in hover can be viewed as a reduction in the rotor induced velocity (at a constant thrust and height above the ground) by a factor kc such that

" Power required IGE "		Г Pige
Power required OGE	T =const	L POGE.

P IGE

This means that up to a 25% reduction in the induced velocity and the induced power is possible with the Cheeseman & Bennett model.

Using a relatively simple model, Betz (1937) has suggested the effect on the rotor power at a constant thrust to be modeled by the equation

Hayden (1976) has used flight test measurements to find the influence of the ground in hover. The profile part of the total power was assumed to be isolated from the induced effect such that only the induced effect is influenced by the ground, that is,

P = Pq + кс{Рі)юЕ,

where kc is derived from a curve fit to the experimental data using

with A — 0.9926 and В = 0.0379. As shown by Fig. 5.36, when viewed in terms of an increase in thrust for a given power, Hayden’s result is found to slightly overpredict the rotor thrust. In all cases it is apparent that the effects of the ground on the rotor performance become negligible for rotors hovering greater than three rotor radii above the ground.