Lift and Induced Drag of a Body of Revolution at Angle of Attack

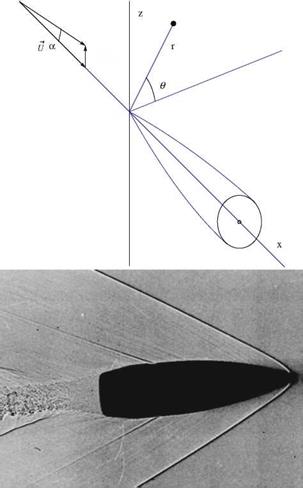
The flow situation is depicted in Fig.7.8. The perturbation potential ф is governed in this case by the three dimensional equation

y

Usin a

Ucos a

0

Fig. 7.8 Body of revolution at angle of attack: Top, coordinate system; Bottom, bullet at supersonic speed (from http://en. wikipedia. org)

The boundary condition is given by

ur dR

ux body dx

In terms of the incoming flow and perturbation velocity, this becomes

U sin a sin в + ^r dR

V U cos a + Ш )body ~ d

Because of linearity, ф can be written as (see Liepmann and Roshko [6])

ф(х, r, в) = ф0 (x, r) + фа(х, r, в) (7.64)

and фа is solution of the full equation that can be modeled as a doublet distribution along the x-axis. The axis of the doublet is parallel to the z-axis to represent the cross flow, namely

дф0 дф0

фа (x, Г, в ) = 0 = sin в 0 (7.66)

with the boundary condition on the surface as

This last equation is obtained to second-order O (a2) from the general boundary condition for ф, upon subtraction of the axisymmetric boundary condition for ф0.

Notice that the first term in the left-hand-side is very small for slender configura­tions. In this case

фа = ^X^ sin в (7.68)

r

The strength of the doublet q (x) is proportional to the cross sectional area

Therefore, the cross flow solution at any section is the same as the incompressible flow solution over a cylinder, independent of M0.

The surface pressure coefficient is given by

2 1 Г / дф2 /1 дф 21

U cos ad x (U cos a)2 dr r дв

and

(7.72)

In the latter expression, a2 terms are neglected.

The normal force in the z-direction can be calculated via integration

N = – p0U2 / f {—Cp, a sin в) Rdedx

2 0 0

1 2 I I 2 dR 1 2

= 4a-p0U2 sin2 в R de dx = 2a-p0U2 S(l) (7.73)

2 0 0 dx 2

Hence, the normal force coefficient, using the base area as reference, is given by

Cn = 2a (7.74)

Notice that, if the body is closed at both ends, N = 0.

The calculation of the drag is more delicate, since it is a small quantity (of order a2). For slender bodies, CL — CN = 2a, independent of M0, and the lift slope is dCL/da = 2 for incompressible and compressible flows.

If one considers a cross section of the body at a given x location and let the circulation be defined on the body as

r(x, в) = ивRde, 0 < в < п (7.75)

—в

then

r(x, в) = фa(x, R, в) — фa(x, R, —в)

= 2фa(x, R, в) = 2U sin aR(x) sin в = 2U sin a^JR2(x) — y2 (7.76)

In term of the “span” variable y, this is an elliptic loading with induced drag Coi = at Cl.

It can be shown that at = a/2 and CDi = a2.

According to Viviand [7], the induced drag coefficient is given by the same formula as for a finite wing

where the surface integral is performed on £base, the part of the cross flow plane outside the base of the body and approximately perpendicular to the incoming flow, Fig.7.9.

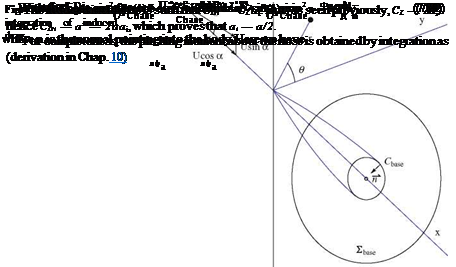
As seen in Chap. 6, this surface integral can be reduced to a line integral along the body base, Chase, as