LIFT CHARACTERISTICS OF SPLIT FLAPS

Split flaps have been used for many years in fighter-type airplanes as a simple device for increasing their glide-path angle and reducing landing speed.

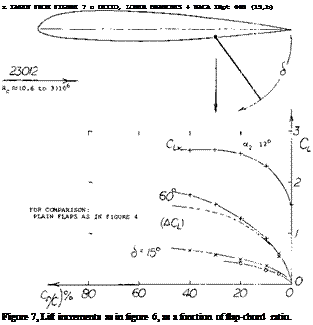
Flow Pattern. At higher angles of deflection me pattern past split flaps is very similar to that of plain flaps. As a consequence, lift as a function of flap angle as in figure 6, is similar to that as in figure 3; that is. above 6 & 25°. In a similar manner, the lift increments m figure 7, for constant angles of deflection, are almost as high as those in figure 4. Referring to the theoretical “analysis” in the first section of this chapter, equation 3 can be applied to interpolate lift increments using &/2 and siri(6/2). Fig­ure 7 reveals, however, that split flaps are somewhat superior to plain flaps. The straight upper side of the airfoil section evidently leads the flow right to the trailing edge, while past a plain flap the flow is exposed to interference (mixing) with the highly turbulent “dead” space. Another advantage of the split type might also be a more stable wake pattern; the separation points are clearly fixed.

Zap Flap. A linkage system is shown in figure 8, through which the split flap can be moved back when deflecting, or be deflected when moving its pivot point back. The advantages are a reduction of actuation forces and an increase of effective wing chord. The corresponding incre­ment of lift may be found in figure 9, as a function of the distance of translation. Assuming that it would be correct to say that in figure 7, the increment increases as (aCl ) ~ v/c7/c, it may also be stated that

(дСц) l/c77c0 (10)

However, as we will see below, the lift-curve slope in­creases also corresponding to the effective chord length (c + лх). A more basic formulation, therefore, is necessary.

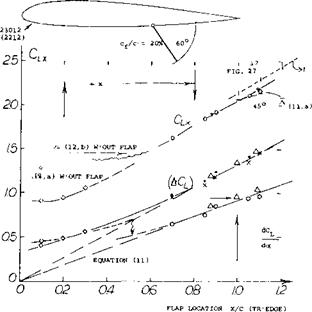
Split Flap Forward. As shown later, the nose-down pitch­ing moments due to trailing-edge wing flaps are large. To reduce them and possibly to make it practical to use split flaps as glide brakes it has been tried to locate such flaps more forward. In figure 9, lift characteristics are shown of a split flap for various flap positions “x” along the lower side of a rectangular wing. Considering the most “stable” range, say at at around 8°, extrapolation of the straight – line lift coefficients to CL = zero, leads to an approxi­mately common angle of attack. For the 20% flap, this angle corresponds to л оt ъ -15 , as measured against that for the plain foil section. Such common angles are also found in (12,b) for flap angles different from 60 and for chord ratios other than 20%.

(9) Investigation of perforated (brake) flaps:

a) Purser, Split Flaps on 23012 Wing, NACA W Rpt L-445 (1941).

b) Purser, Brake Flaps 33% Perforated, NACA W Rpt L-415 (1943).

Lift-Curve Slope. It may be argued that when moving the flap’s hinge point forward, the effective airfoil chord corresponds n( irly to that indicated by the trailing edge of the flap when folded, since the flow is fully separated from the lower side of the wing, with the flap deflected. In two-dimensional flow, thus approximately:

dCL/dof — (с + 4x) ^ (1 + (дх/с)) (11)

where x as defined in figure 9. After subtracting for the results as in (12), A(dof /dCL) = 3.5 for induced and affiliated considerations, two-dimensional lift angles doc /dCL are obtained. As shown in the illustration, the corresponding lift-curve slopes vary approximately as in equation 11. For example, for the angle of attack (in two-dimensional flow) where the lift of the plain foil section is zero, theoretical (dCL ) values are obtained for the flap arrangements in figure 9. Plotted together with values directly evaluated from 12, a variation essentially in proportion to that in equation 11 is found.

Full Scale Airplane. A systematic series of almost full-span split flaps is reported in (12,b). This investigation has the advantages that it has been conducted on a real airplane (in the NACA’s Full-Scale Wind Tunnel). We have cor­rected the results to full-span condition, using the part – span functions presented later and have reduced these results to two-dimensional conditions as explained above. For a 20% and 60° flap, the extapolated zero-lift angle is found to be displaced by Aot = —11° , and -15° respec­tively that is, after correcting for the flap cutout in the center of the parasol-type wing. Corresponding values for other flap chords and other deflection angles vary ap­proximately in proportion to the statistical functions as in figure 6 and 7, respectively. The lift-curve slopes vary in proportion to that in figure 9, or as indicated by equation 11.

(10) Characteristics of simple split flaps:

a) Goett; 0009,12,18 Wings in Full-Scale Tunnel, NACA TRpt 647 (1939).

b) Wenzinger, 23012,21,30 Wings With Various Flaps, NACA TRpt 668 (1939).

c) Fullmer, On 66-216 and 65-212 Foil Sections, NACA W Rpt L-140 (1944).

d) West, Presentation of the Characteristics, J. RAS 1940 p 338.

e) Williams, Wings in the Compressed Air Tunnel, ARC RM 1717 (1936).

f) Schrenk (AVA), Split Flaps to = 120 , ZFM 1932 p 597.

g) Wenzinger, Tapered Wing with Split Flaps, NACA TN 505(1934).

о A = 6, RECTANGULAR, 6(10)5 (12, a) / ^ • DITTO, DIRECTLY EVALUATED

X DITTO, CALCULATED (SEE TEXT)

Д PARASOL AIRPLANE AT 3(10)6 (12,b) П + DITTO, MAXIMUM LIFT IN FS TUNNEL О WALLS, 60° PERFORATED FLAPS (’ft, a ) <7

Figure 9. Lift coefficients of rectangular wings with A = 6, tested with 20% split flaps in various chordwise positions.

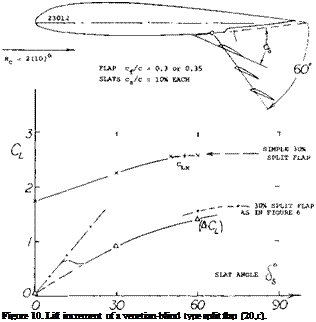
Perforated Flaps. A discontinuity in the (aCl) function is found in figure 6, at 6 between 20 and 30е5. It is suggested that below this range, a “simple” viscous wake is formed behind the split flaps tested, while above S & 25 , a Karman-type vortex street is established. This ex­planation is confirmied by a corresponding discontinuity in the section-drag coefficient, showing a step-up ACD5 # 0.01, which is ACD = 0.1 based on “base” area of the flap. The change in flow pattern is also confirmed by a step in the maximum lift coefficient as found in (16,a) for several split flaps, at some angle 6 between 15 and 30°. This step is in the order of лСих = —0.1. An up and down swinging wake can induce lift and drag fluctuations in the wing; and it can cause serious vibrations in the horizontal tail of an airplane. Figure 10 shows one of many “venetian-blind” type split flaps investigated in (20,c). Around 6s = 15°, the flow can be expected to separate from the slats. Another way of breaking up the wake into smaller vortices, is by means of perforated flaps. Characteristics of such flaps (plates) are reported in (9). Lift due to flap must be expected to reduce as a function of the solidity ratio S./Sf. For example, when removing 1/3 of the solid flap surface, flap load (normal force) and effectiveness (ziCL) are reduced roughly to 2/3.

Airfoil-Section Shape. Split flaps can easily be attached to wind-tunnel models. This was evidently the inducement for testing routinely (13) various airfoil sections with a standardized 20% and 60° split flap. Such tests are con­sidered to indicate the forebody response to trailing-edge flaps in general, corresponding to thickness ratio and other shape parameters. Evaluation of (13,a) shows that camber between 0 and 4% of the chord has practically no influence on the increment (aQ_ ). One of the parameters describing shape is the location of maximum thickness. The due-to-flap increment increases as this location “x” is moved back along the chord. Thus as tested at Rc = 6(10) (with roughness strips added near the leading edge):

20%, 60° SPLIT FLAPS

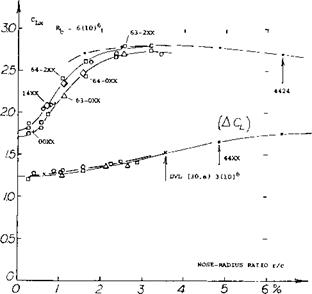
It is seen in figure 12, that when plotted against r/c, certain families of airfoil sections show approximately the sameACL, lift-due-to-flap values. The increment (ACl) increases from 1.25 for sharp-edged sections, to a possible maximum of 1.8 at radius ratios above r/c = 6%. Since the nose radius increases in proportion to the square of the section thickness, it can be argued that according to theory (see Chapter II ) that the lift-curve increases with the thickness ratio. For the maximum represented in the graph (t/c = 24%) the increment would be some 19%. The desirable effect of the high leading edge radius illustrates the importance of protecting the leading edge from sepa­ration so that high values of CLx can be obtained both with and without flaps. This is further discussed in the next chapter on leading edge devices.

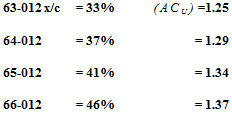The nose radius of a certain foil section is indicated by r/t = К t/c

where К = 1.1 for NACA 4-Digit sections, or К = 0.76 for the 63 Series, decreasing to 0.70 for the 65 Series. The radius thus varies as

r/c = К (t/c/ (13)

(11) Discussion and characteristics of Zap flaps:

a) Weick, Split Flap Moved to Rear, NACA TN 422 (1932).

b) Joyce, Discussion of Zap Flaps, Trans ASME 1934 p 193.

c) Serby, Balancing of Flaps, Aircraft Engineering 1937 p 292.

d) Dearborn, Fairchild Airplane with Zap Flap, NACA TN 596 (1937).

e) Jones, Full-Scale Flight Tests, ARC RM 1741 (1936).

0 Practical Discussion, “Flight” Supplement 27 July and 31 Aug 1933.

(12) Characteristics of split flaps moved forward:

a) Wenzinger, 23012 Wings With Split Flaps, NACA TN 661 (1938).

b) Wallace, Fairchild Airplane With Split Flaps in Full-Scale Tunnel, also flap loads and downwash, NACA TN or TRpt 539 (1935).

c) The Schrenk flap (15,f) is also investigated in the CAT, ARC RM 1636.

(13) Influence of airfoil shape on flap effectiveness:

a) Abbott-vonDoenhoff-Stivers, Airfoil Data, NACA TRpt 824 (1945).

b) DVL, Collection of Berlin Airfoil Data, ZWB FB 1621 (1943).

c) Loftin, Modified 4-Digit Sections, NACA TN 1591 (1948).

d) Loftin, 15 Airfoil Sections, NACA TN 1945 (1949).

e) Loftin, 6A-Series Airfoil Sections, NACA TRpt 903 (1948).

(14) The flow pattern of slotted flaps:

a) Hoerner, Wing Flaps, Fieseler Water Tunnel Rpt 11

(1939) .

b) Petrikat, Landing Flaps, Fieseler Water Tunnel Rpt 19

(1940) .

Figure 11. Lift increment in two-dimensional flow due to standard 20% and 60 split flap, as function of the nose-radius ratio.

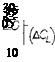Figure 12. Lift increment in two-dimensional flow due to standard 20% and 60 split flap, as a function of the trailing-wedge angle (thickness ratio at 80% of the foil chord).

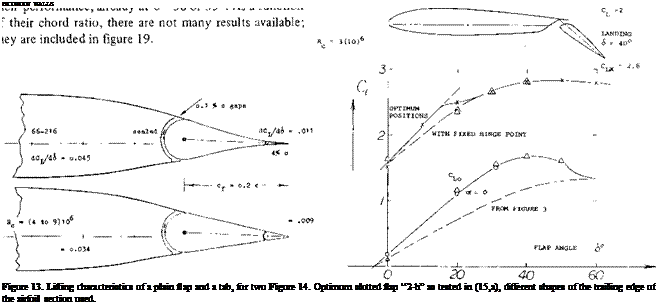
Plain Flaps. The influence of the trailing-wedge angle as for split flaps, does not necessarily hold for other types of flaps such as conventional plain flaps. Figure 13 presents the example of an aileron flap and a tab, attached to a 66-216 airfoil section. From what is said in Chapter IX on control devices it is clear that at small angles of deflection, the thin-edged flaps have greater effectiveness. Both the aileron and the tab show each some 25% higher (^Cu) values for the cusped section shape. Considering higher angles of deflection (tested to 25 only) where the flow is no longer attached to the back of the flap, the configura­tion as in figure 13, indicates increments higher by

17% for the aileron,

19% for the tab flap,

when using the concave shape. These variations are con­trary to those found for split flaps. There are two reasons to be considered. Plain flaps, with their hinge point lo­cated on section center line, do not grow effectively longer when deflected. Also, the geometrical angle of the flap at the lower side and near the trailing edge, is some­what larger for the cusped than for the straight-sided shape.