Noise from Fine-Scale Turbulence

Traditional theories of aerodynamic noise and the development of their mathematical foundations were described in Section 3.1. These methods require a detailed knowledge of turbulence, which is then used as input for noise calculations. Therein lies the fundamental difficulty in these ap­proaches. Despite nearly a century of turbulence research, our understand­ing of turbulence and the development of accurate models for the turbulence statistics are still remote. Given this situation, it is perhaps not surprising that most existing methods[5], which make use of some model for the statis­tical properties of the turbulence, fail to capture the spectral characteristics of jet noise at all angles.

Tam (1995b) and Tam (1998b) have provided a different perspective on jet noise. As described in Section 3.2, Tam and Morris, among others, have had success in predicting the large-scale structure noise of circular and non-circular jets using an instability wave model. Following the arguments presented in the previous section that the turbulent mixing noise consists of two components. Tam and Auriault (1999) proposed a model, not formu­lated as an acoustic analogy, for the fine-scale noise component. Drawing an analogy with the kinetic theory of gases, they reasoned that the fine-scale turbulence exerts a pressure on its surroundings, which must be balanced by the pressure and momentum flux of the surrounding fluid. Since this pressure fluctuates in time, it will lead to compressions and rarefactions in the fluid, resulting in acoustic disturbances. They argued that the time rate of change of this pressure in the moving frame of the fluid would constitute the source of the fine-scale turbulence noise. They also argued that the propagation of the resulting sound waves through the jet flow can be de­scribed by the Euler equations linearized about the jet mean flow. It should be noted that, if the mean flow is taken to be parallel, the linearized Euler equations are equivalent to the propagator provided by Lilley’s equation. Tam and Auriault (1999) obtained the Green’s functions for the linearized Euler equations in terms of their adjoint solutions. Details of the use of the adjoint solution to calculate refraction effects in sheared mean flows are given by Tam and Auriault (1998). The method is quite novel, though it is not without difficulties. The cause of the difficulties is the presence of Kelvin-Helmholtz (K-H) instabilities. Both the physical problem and its adjoint have these convective instabilities. It is possible for these unstable solutions to dominate over and obscure the part of the solution associated with sound wave propagation. Tam and Auriault (1998) acknowledged their presence and, in order to avoid these instabilities, they introduced damping functions and damping regions to suppress them. Agarwal et al. (2004) have shown how the instability can be suppressed if a frequency domain formulation is used for the adjoint Green’s function.

Tam and Auriault (1999) showed how the pressure fluctuation outside the jet could be related to the convolution of the adjoint pressure and the

convective derivative of their source term. The formula for the pressure fluctuation is given by,

p (x, t) = J – J Pa (xi, x, u) exp [-iu (t – ti)] du

(55)

where pa (x1, x, u) is the time harmonic adjoint pressure, qs = 2pks/2, and ks is the turbulent kinetic energy of the fine-scale turbulence per unit mass. An expression for the autocorrelation of the intensity can then be obtained and the far field spectral density is obtained using Eqn. (19).

As in noise prediction models based on the acoustic analogy, it is nec­essary to specify a mathematical expression for the noise source space-time correlation function. Tam and Auriault (1999) assumed that the source cor­relation had the same characteristics as the measured two-point space-time correlation of the fluctuating axial velocity in a jet. Morris and Farassat (2002) have shown that there is no essential difference between models based on the acoustic analogy and the predictive model developed by Tam and Auriault (1999) 5. The key difference in the resulting prediction formulas lies in the model used to describe the two-point space-time correlation of the source function. Tam and Auriault (1999) showed that the spectral density can be written,

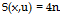
exp [-u2£2s/ {u2 (4ln2)}] 1 + u2t2 (1 – u cos в)

(56)

where u is the local mean velocity and в is the polar angle relative to the downstream jet axis. This formula contains three parameters associated with the fine scale turbulence: a typical length scale £s, a time scale Ts, and a measure of the intensity of the fluctuating kinetic energy A2 q2, where q = 3 pk, p is the mean density and k is the turbulent kinetic energy per unit mass. Tam and Auriault (1999) used the modified k – є model of Thies and Tam (1996) to obtain these three characteristic parameters. Since the k – є model also includes the contributions from the large-scale turbulence, they proposed to extract the fine-scale turbulence contribution through the use of constants with values of less than unity. That is,

£s = в£ (k3/2/є), ts = cT (k/є) : в£ = 0.256, cT = 0.233

Though the modeling philosophy and details of the analysis are different.

where є is the viscous dissipation rate. The values of these constants, and a third constant to set the absolute level, were determined by a best fit of the predicted noise to measured data.

There are three major steps involved in this prediction method. First, the jet mean flow field and the turbulence properties к and є, are computed. In the second step, the adjoint Green’s function is evaluated using the jet mean flow field. Finally, the radiated noise is calculated by adding the noise contributions from each volume element in the computational grid.

Tam and Auriault (1999) show good agreement of the predicted noise spectra with measured data for cold jets at both subsonic and supersonic Mach numbers: however, there are some discrepancies at the very high frequencies. The ability of the model to predict the spectral variations with radiation angle for a Mach 2.0 isothermal jet is also demonstrated. This model also captures the effect of jet temperature on radiated noise. Finally, they show good comparisons of the peak spectral levels for a wide range of jet operating conditions. Tam et al. (2001) show additional test cases for cold jets embedded in a freestream, with good predictive capability. It should be emphasized that this theory makes absolute noise predictions; intensity, directivity, as well as the spectral characteristics of the measured data are reproduced. Of course this is a semi-empirical theory because of the three new constants in addition to the empirical constants inherent in the к – є turbulence model. Importantly, it should be noted that Tam and Auriault (1999) limit their predictions to angles close to 90° to the jet axis. They argue that noise at other angles, particularly in the peak noise direction at small angles to the jet downstream axis, depend on noise from the large-scale structures. So, fine-scale turbulence noise predictions would not be relevant at other angles. Similar findings were obtained by Morris and Farassat (2002) and Morris and Boluriaan (2004) using an acoustic analogy based on the linearized Euler equations.

This model is not without critics. Ribner (2000) questions the validity of the two similarity components and the approach adopted by Tam and Auriault (1999). However, it should be noted that there is a vast amount of experimental data that has established the presence of large-scale structures and their Mach wave radiation. In addition, examination of the expression for the spectral density, Eqn. (56), shows that the jet temperature does not appear explicitly in the integrand. Fisher (38) pointed out that since the dipole term that occurs in classical approaches based on the acoustic analogy is not included, this model should not be able to predict the noise from hot jets.

It should also be noted that there is no convective amplification of the fine-scale turbulence noise in the model of Tam and Auriault (1999). This is not a result of the use of the fixed frame of reference description of the source statistics. The result is independent of the reference frame for consistent source descriptions. Morris et al. (2002) show that if a Gaussian model is used to describe the source correlation in the Tam and Auriualt model, convective amplification appears: but, with only three inverse powers of the modified Doppler factor, rather than the five appearing in models based on the acoustic analogy, such as given by Eqn. (31).