Numerical Results and Discussion

1.3 Unsteady aerodynamic Work on Oscillating Blades

The results presented in this paper are restricted to cases where blades of rotor 1 (located upstream) are vibrating in a bending mode. The blade dis­placement function is assumed as

where h1 (r) denotes the mode shape of bending displacement of order 1 of a uniform canti-lever beam. In all cases the axial Mach number and the boss ratio are fixed to Ma = 0.6 and h = 0.7 respectively. Further four cases shown in Table 2 are dealt with. Note that the relative fbw velocity for the rotor blades is supersonic along the whole span for i| = 3.0 or |fi2| = 3.0, and subsonic along the whole span for |fi1| = 1.0 or |fi2| = 1.0. In all cases the distance between the blade raw centers is fixed to G = 2.0Ca, where Ca = (Cal + Ca2)/2.

Table 2. Specified conditions

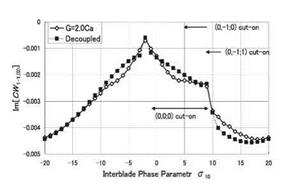
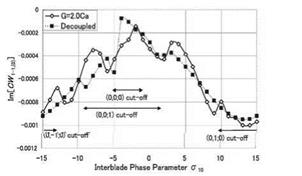
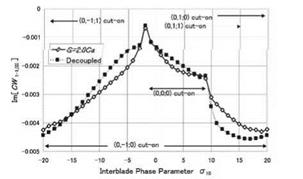
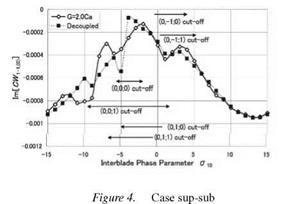
Figures 2 – 5 demonstrate unsteady aerodynamic work coefficient S[CW1-1)(0) ] as a function of the interblade phase parameter a10 at a reduced frequency uCa1 = 0.5. In each figure comparison with the aerodynamically decoupled case (an isolated rotor cascade) is shown. Cut-on or cut-off regions of relevant duct modes are also indicated in the figures. First of all it should

be pointed out that duct modes (-1,1; i) and (1, -1; i) of i = 0 and i = 1 are cut-on in the whole region of a10 in all cases. As a phenomenon common to both cases sub-sub (Figure 2) and sub-sup (Figure 3) the infhence of the neighboring blade row, i. e., the difference in the aerodynamic work between the case of decoupled blade row and the case of coupled blade rows, is large

Case sub-sup. Modes (1, -1; £) and (-1, 1; £) of £ = 0, 1 are cut-on everywhere

in the region where the main duct mode (0, 0; 0) generated from rotor 1 is of cut-on state. Note that in the case of the decoupled blade row, this mode is one and only one cut-on duct mode at the specified reduced frequency. In addition strong inflience is also seen in the regions where duct modes (0,v, t) of v = 1 or v = —1 regenerated from rotor 2 are cut-on. In case sub-sup (Figure 3) where rotor 2 cascade is supersonic, a large number of duct modes are of cut-on state, and on the whole the infhence of the neighboring blade row is higher than in case sub-sub (Figure 2). It would be worth emphasizing that at the resonance points of the duct mode (0,0; 0) the curves of the aerodynamic work show sharp bends, but the difference between the decoupled cascade and the coupled cascades is remarkably small.

In cases sup-sub (Fihure 4) and sup-sup (Figure 5) where rotor 1 cascade is supersonic most of the duct modes are cut-on and the number of cut-off duct modes is small. Near the resonance points of duct modes (0,0; 0) and (0,0; 1) which are originally generated from rotor 1 cascade the curves of the aerodynamic work show humps, but in contrast to cases of subsonic rotor 1 cascade (Figure 2 and 3) no coincidence in the aerodynamic work between the decoupled blade row and the coupled blade rows is observed at resonance points, and the difference is rather large around the resonance points. The curves for the coupled blade rows show more complicated variation with а ю than those for the decoupled blade row because of appearance of resonance points of duct modes (0,v; t) with v = 0 which are regenerated from rotor 2 cascades.