PERFORMANCE DURING TAKEOFF AND CLIMB

Although flaps are usually designed for the landing condi­tion, higher lift coefficients will also make possible im­proved performance during takeoff and climb. At these conditions drag becomes an important consideration as the performance is determined by the level of excess thrust. Thus, for improved takeoff and climb performance it will be found that flaps with higher levels of CL* and lift drag ratio are needed.

Flow Pattern. To determine the best flap configuration, it is desirable to understand the flow pattern in and around the flap. Unfortunately, when watching wind-tunnel tests one sees very little. Examination of the drag – and lift forces as tested, and sometimes pressure distributions, will give some indication of the actual flow pattern. For ex­ample, flow separation from the upper side of the flap shows up in reduced lift, increased drag and (if tested) in higher hinge moments. However, some investigations of slotted flaps have been undertaken (14) in a water tunnel where the flow pattern was visible while measuring forces and moments at the same time. Some results are presented in figure 21.

a) In neutral flap position, there is a stationary small vortex within the slot entrance. Such a vortex consumes little energy, provided that the outlet of the slot is ef­fectively closed (sealed).

b) For the slot shape as shown, the flow separates around the bend of the entrance. As long as this separation is only local, an efficient nozzle flow may develop, as long as the flow remains essentially attached to the upper side of the flap.

c) A bad example of a flow pattern is shown for a deflection angle of 50°. Separation is “complete” within the slot as well as on the upper side of the flap.

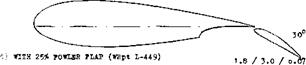
Optimum or acceptable slot and flap shapes are discussed below. However, the only straight-forward way of making a single-slotted flap really efficient is to give it a long and flat entrance. In a way, this is done in the case of the Fowler flap (to be discussed later).

Thick Wing Sections. For a certain period of time, sec­tions with thickness ratios in the order of 20% were used. It seems that someone put together the facts

that minimum drag of thick sections (when tested on

smooth wind-tunnel models) is not much higher than

that of wings with conventional thickness ratios,

that very high aspect ratios may result in low induced

drag and long range,

that thick wings could be used to store fuel, as in long-range airplanes.

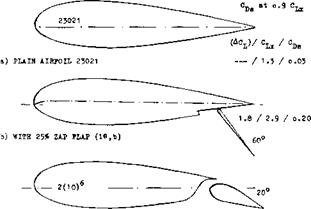
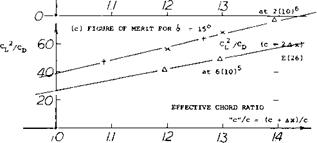
It was therefore found justified to spend money on the tunnel testing of airfoil sections up to t/c = 30% such as in (16c, e,f)- It is interesting to see to what limits one can go in aerodynamic shape. To increase the maximum lift co­efficient of such sections, slotted flaps have been tried (15,d, e,f). The general characteristics of their performance are given in figure 22. The choice of the flap type for these thick sections can be evaluated from a comparison of Cuy and L/D @ CL = .9CLX* Based on this the double slotted type is superior because of the reduced separation and drag.

і

Thrust Available. The takeoff and climb performance is directly a function of the excess thrust available as shown by equation

wc – (T/W – D/W)V = (T/W – 1/(L/D))V

Since the thrust available is here considered to be fixed, the thrust required must be determined and minimized for best performance. The excess thrust is the difference in that available and the total drag. On the ground the drag includes the ground rolling friction, the “parasitic” or

o) WITH 26* SLOTTED FLAP (16 ,a) 1.0 / 2.4 / o.06

viscous components, the ideal induced drag and that in­duced component due to the non-elliptical loading. When considering flap performance during takeoff and climb, the drag increase due to deflection and the non-elliptical loading are of primary concern. Also of importance is the maximum lift coefficient at the flap setting being con­sidered.

Figure of Merit-T. O. In Chapter I a figure of merit was given for evaluating configuration with respect to the takeoff and climb performance. The peak climb angle is obtained when Cq /cf. , the figure of merit, is a mini­mum. The drag coefficient corresponds to the total at the CL selected. While the value of CD /CL gives a rough idea of the relative merit of a system it does not indicate the full capability, as the CL is not known for the system. A better procedure is to relate the performance to C and the operating rules governing takeoff.

Takeoff Characteristics. The performance at takeoff in terms of field length and maximum gross weight is gov­erned by safety considerations and the corresponding op­erating rules and regulations (19,a, b). These con­siderations generally lead to a requirement of a minimum rate of climb after takeoff with the flaps and landing gear in the takeoff configuration. The rate of climb required must usually be met with the critical engine inoperative. Where the case where power is fixed equation can be rewritten in terms of the lift drag ratio required

L/Dy = 1/(T/W – wc /V) (26)

At the L/Dr given in equation 26 the airplane is generally required to operate at a speed 20% above the stalling speed. This means that the operating Cu is 1/1.44 CL)C for the flaps and landing gear in the takeoff configuration. Thus the takeoff speed is effected by two considerations: the L/D ratio and the CLx. If the flap angle could be changed during takeoff improved performance would be possible, but this is not allowed by the rules and is generally impractical as the pilot work load during a failure is too high.

Figure 22. Lifting characteristics of 21% thick airfoil sections, tested between walls at Rc = 2(10) , equipped with various types of flaps.

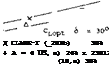
Flap Selection for Takeoff Flaps are usually thought of as devices for improving the maximum lift coefficient and are thus selected for reducing the landing distance. On most conventional powered jet aircraft, however, the field length needed for takeoff is generally longer than that required for landing. Thus, the flap system should be designed to give peak takeoff performance as well as minimum landing distance. Based on the concept of op­erating at a CL that results in the L/D needed to give the required rate of climb at takeoff, the best flap configura­tion and operating angle can be found. This requires determining the lift drag ratio for the complete airplane as a function of flap angle when operating at a CUp = CLX /1.44. The choice of the best flap type and angle for takeoff can be determined from plots such as illustrated on figure 24. On figure 24,a the lift drag characteristics of the total airplane are given as a function of flap angle for various types of flap configurations with NACA 6 series sections (13,a). The lift coefficient corresponding to the flap angles is given on figure 24,b for the same section. Based on a given L/D required to satisfy the climb require­ments the lift coefficient at takeoff can be determined for the given system from figure 25. The flap angle is then found from figure 24,a at the same lift drag ratio and flap type. From these figures the best flap’system is obtained when at the L/D. Based on the data given on figure 24 the double slotted flap is the best of these considered as it generates the highest coefficient for any given lift drag ratio.

Part-Span Flaps have been mentioned above. In a rec­tangular wing, a modest inboard flap deflection can be expected to reduce the induced drag during climb (28 ,e), making the lift distribution more elliptical. In conven­tionally tapered wings, the induced drag is likely t:o be increased. There are elaborate methods available (22) for the determination of load distribution across the span. An approximate procedure of estimating the corresponding variation of the induced drag is presented in Chapter VII of “Fluid-Dynamic Drag”. Another such method is as follows.

Induced Drag. An analysis of elliptical wings with part – span flaps is presented by Young (5,f). For practical purposes it can be said that

c0i = (Cl / ТГА) + K(ACl ) (33)

where C = coefficient of toal lift, and лСь = (&CL) Sf/S, where (ЛС|_) = increment due to flap in two – dimensional flow as in various graphs of this chapter. The factor К is approximately as follows:

К =0.17(1 — (bf/b)) for inboard flaps

= 0.21 (1 — (bf /b)) including a 0.1 b

cut-out

4

G

(b) OPTIMUM LIFT

Figure 23. Performance of extended-lip slotted flaps (including Fowler flaps) as a function of their translation.

where bf is measured between the ends of the flaps. For example, for bf/b = 0.5, the factor К is ^ 0.04, and^

0. 05 when including 10% cut-out due to the fuselage. It is interesting to note that for a given combined geometric flap span (not including the cut-out) the minimum in­duced drag of elliptical wings is obtained for a cut-out in the order of 10% of the span. As mentioned before, the increments due to flaps, particularly in rectangular wings, are different from those of the elliptical ones stated in this paragraph. We will assume, however, that the basic lift distribution may be close to elliptical, as it actually is in average tapered wings.