PITCH STIFFNESS OF A GENERAL CONFIGURATION
Having established above the central importance of the derivative C for satisfactory flight, we turn now to a detailed discussion of it for a general vehicle configuration. We consider the vehicle to be composed of a body, a wing, a tail and propulsive units. If any of these are absent (as for a tailless airplane, a wingless missile, or a glider) the appropriate deletions from the analysis are readily made.
The pressure distribution over the surfaces of a vehicle in steady rectilinear motion, and the consequent integrated forces and moments, are functions of angle of attack a, control surface angles, Mach number M, Reynolds number Re, thrust coefficient CT, and dynamic pressure pV2. The last-mentioned parameter enters because of aeroelastic effects. If the vehicle is flexible, then a change in dynamic pressure, with all other variables constant, produces a change in shape, and hence of the forces and moments.
In the following discussion the only restriction in relation to the above parameters is that of steady rectilinear flight. Specifically, power effects, flexibility, and compressibility effects are not excluded.
PITCHING MOMENT OF A WING
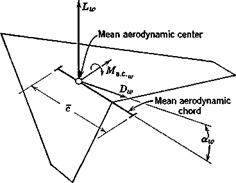
The force system acting on an isolated wing, in symmetric flight, can be represented as a lift Lw and drag ])w acting at a reference point, the mean aerodynamic center, together with a pitching moment Ma c (Fig. 6.7).
|
Fig. 6.7 Aerodynamic forces on the wing. |
|
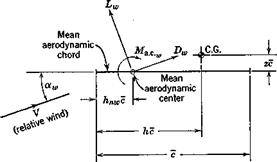
Fig. 6.8 Moment about the C. G. in the plane of symmetry. |
The inviscid theory of thin wings at small aw predicts that the moment about the aerodynamic center is invariant with aw, and this is indeed very often the case in reality. However, it is possible that „ may vary with aw, and this case is included in the following. The moment of the force system of Fig. 6.7 about the vehicle center of gravity (see Fig. 6.8) is given by
= – Ma. c.„ + (Lw cos ocw + Dw sin am)(h – hnJc
+ (La sin a„ – Dw cos xjzc (6.3Д)
For many flight situations, including the cruising flight of all classes of fixed-wing aircraft, the angle of attack is small enough to justify the approximations sin am = aw, cos aw = 1. We take this to be the case here, bearing in mind the consequent restriction on the validity of the resulting equations.
Equation (6.3,1) is made nondimensional by dividing through by %pV2Sc. It then becomes
Cmw = ^ma. c.„, + ^Dwaw)(^ — У + — CDf)z (6.3,2)
Although it may occasionally be necessary to retain all the terms in (6.3,2), experience has shown that the last one is frequently negligible, and that Gnjy. w may often be neglected in comparison with CLw. With these simplifications, we obtain
Ста = Стлс +CLJh-hnJ (6.3,3)
* ‘to
Equation (6.3,3) will be used to represent the wing pitching moment in the discussions that follow.